I triangoli sono insiemi di punti nel piano formati da una poligonale chiusa di tre lati e dei suoi puntio interni.
In pratica il triangolo è una figura geometrica formata da 3 lati la cui somma degli angoli interni è 180°
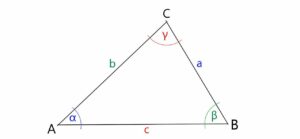
α + β + γ = 180°
In un triangolo un angolo è detto adiacente ad un lato quando uno dei due lati dell'angolo è il lato in questione. Ad esempio nella figura in alto il lato AB è adiacente all'angolo α e all'angolo β
In un triangolo sono individuabili:
L'altezza è relativa ad un lato, è perpendicolare al lato in questione e unisce il lato con il vertice opposto.
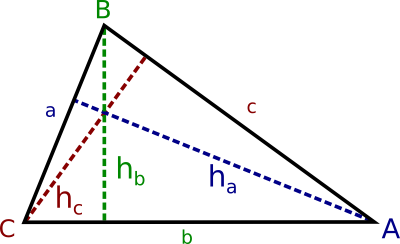
Essendo che le altezze formano un angolo di 90° con il lato, creano dei triangoli rettangoli all'interno del triangolo stesso. Le varie altezze si possono calcolare usando il teorema di Pitagora
La bisettrice è il segmento che congiunge il vertice al lato opposto.
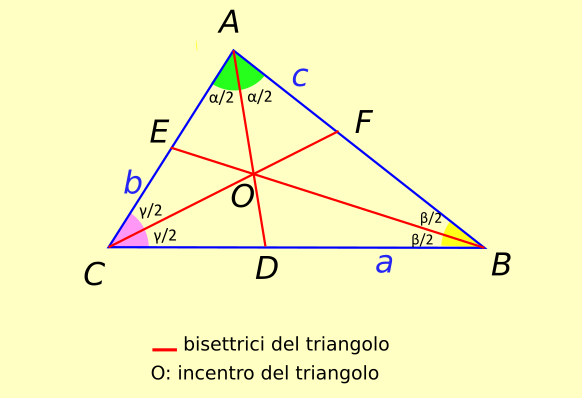
La mediana è il segmento che unisce il punto medio di un lato con il vertice del lato opposto

I triangoli possono essere di tre tipi per LATO:
- Equilatero: ha tutti e tre i lati uguali
- Isosciale: ha due lati uguali e uno diverso
- Scaleno: ha tutti i lati diversi
E per ANGOLO:
- Acutangolo: ha tutti gli angoli acuti (più piccoli di 90°)
- Ottusangolo: ha un angolo ottuso (più grande di 90°)
- Rettangolo: ha un angolo retto (90°)
Due triangoli si definiscono congruenti tra di loro se rispettano uno di questi due criteri:
Per il primo criterio due triangoli sono congruenti tra di loro se hanno ordinatamente due lati congruenti e l'angolo tra essi compreso. "ordinatamente congruente" significa che i lati devono essere congruenti ai corrispettivi nell'altro triangolo
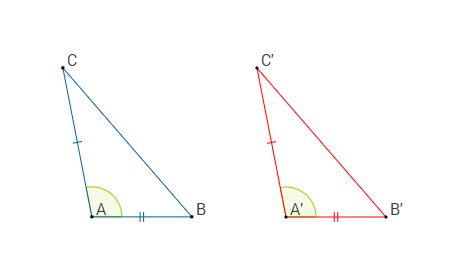
Ad esempio in questa immagine
- AC è congruente a A'C'
- AB è congruente a A'B'
- L'angolo A è congruente all'angolo A'
Quindi, per il primo criterio, i due triangoli sono congruenti.
Per il secondo criterio due triangoli sono congruenti se hanno ordinatamente congruenti un lato e i due angoli adiacenti al lato.
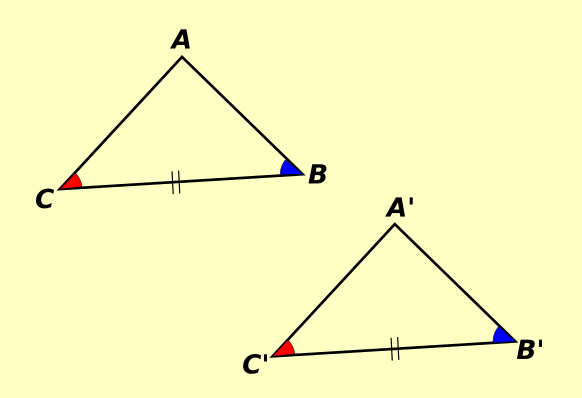
Ad esempio in questa immagine
- BC è congruente a B'C'
- L'angolo B è congruente all'angolo B'
- L'angolo C è congruente all'angolo C'
Quindi, per il secondo criterio, il triangolo ABC è congruente al triangolo A'B'C'
