Se definiamo una quantità fisica Aα tale che valga la seguente uguaglianza
![]()
Aα è definita tensore se l’uguaglianza rimane invariata dopo un cambio di sistema di riferimento.
Quindi la trasformata di Lorentz di (in funzione di la possiamo scrivere in questo modo:
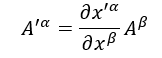
I tensori vanno sempre indicati con delle lettere (generalmente lettere greche) messe ai pedici o agli indici, le lettere messe all’apice sono le coordinate controvarianti mentre le lettere poste all’indice sono le coordinate covarianti.

I tensori sono rappresentati da matrici, quindi l’uguaglianza vista prima diventa
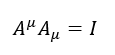
Per un tensore con sia coordinate covariante che controvarianti si scrive in questo modo:
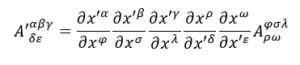
Gli indici covarianti vanno scritti al denominatore mentre gli indici controvarianti al nominatore e vengono scritti per indicare tutti i possibili valori di quel tensore
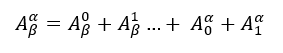
Che si può riscrivere facilmente in questo modo:
![]()
Operazioni tra tensori:
- Somma tra tensori che creano un nuovo tensore
![]()
- Prodotto tra tensori che creano un nuovo tensore
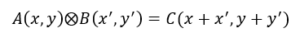
- Che si può scrivere anche in questo modo:
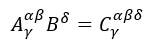
- “Semplificazione” tra due indici uguali di un tensore
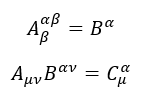
La derivata covariante è la derivata di un tensore e viene usata per trasformare una derivata di un’equazione in relatività ristretta in un’equazione valida in relatività generale
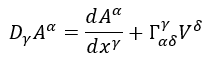
Una derivata covariante uguale a 0 non implica nessuna conservazione.
