- Esercizio 1 (tensione singola)
Sul lampadario agiscono due forze; la forza peso verso il basso e la tensione del filo verso l'alto che bilancia il peso. Di conseguenza per poter mantenere l'equilibrio le due forze opposte devono essere uguali
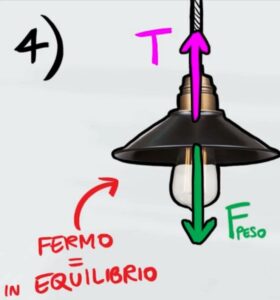
$F_p=T$
Da qui ricaviamo la tensione
$T=mg=28,43N$
- Esercizio 2 (tensione doppia)
Per poter restare in equilibrio la somma delle forze verso l'alto deve bilanciare la forza peso verso il basso
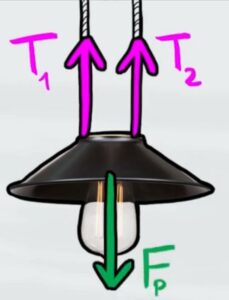
$T+T=F_p$
Ora basta risolvere questa equazione per ricavare la tensione T
$2T=F_p$
$T=\frac{F_p}{2}=\frac{mg}{2}$
La massa è la stessa del problema di prima, ovvero 3kg. Facendo i calcoli otteniamo
$T=14,715N$
- Esercizio 3 (due tensioni inclinate)
Per prima cosa dobbiamo scomporre le tensioni nelle componenti x e y
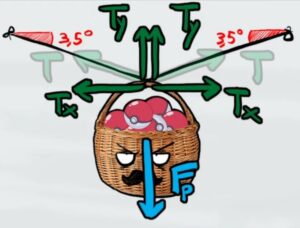
Per avere l'equilibrio tutte le forze sull'asse x devono essere 0 e tutte le forze sull'asse x
EQUILIBRIO ASSE Y → $T_y+T_y-F_p=0$
EQUILIBRIO ASSE X → $T_x-T_x=0$
L'equilibrio sull'asse X ci dice semplicemente che $F_x=F_x$ che è un informazione inutile per il problema. Quindi consideriamo solo l'equilibrio sull'asse Y
$2T_y-F_p=0$
$2T_y=F_p$
In questo modo ricaviamo la componente Y della tensione sapendo che la forza peso del cesto è mg
$T_y=\frac{mg}{2}$
Scriviamo la tensione Y come il prodotto della tensione per il seno dell'angolo
$T_y=Tsin(3,5°)$
In questo modo otteniamo
$Tsin(3,5°)=\frac{mg}{2}$
$T=\frac{mg}{2sin(3,5°)}=160,7N$
- Esercizio 4 (due tensioni inclinate)
Dividiamo le due tensioni nelle componenti X e Y
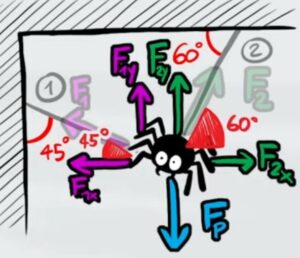
Dall'immagine possiamo vedere subito quali sono le forze opposte tra di loro, quindi possiamo scrivere le condizioni per l'equilibrio sui due assi:
EQUILIBRIO ASSE Y → $T_1sin(60°)+T_2sin(45°)-F_p=0$
EQUILIBRIO ASSE X → $T_1cos(60°)-T_2cos(45°)=0$
Dove $Tsin(α)$ indica la componente Y mentre $Tcos(α)$ indica la componente X.
RICAVARE $T_2$
Per poter risolvere il problema basta risolvere questa serie di equazioni, dall'equilibrio asse X ricaviamo una delle due tensioni:
$T_1=\frac{T_2cos(45°)}{cos(60°)}$
E la sostituiamo nell'equilibrio asse Y
$\frac{T_2cos(45°)}{cos(60°)}\cdot sin(60°)+T_2sin(45°)-F_p=0$
La forza peso del ragno possiamo scriverla come mg
$\frac{T_2cos(45°)}{cos(60°)}\cdot sin(60°)+T_2sin(45°)=mg$
Da questa equazione raccogliamo T_2
$T_2[\frac{sin(60)°cos(45°)}{cos(60°)}+sin(45°)]=mg$
Da questa equazione basta dividere il tutto per il termine che moltiplica $T_2$ e sostituire con i termini numerici per ottenere il risultato
$T_2=\frac{mg}{\frac{sin(60)°cos(45°)}{cos(60°)}+sin(45°)}$
$T_2=0,015N$
RICAVARE $T_1$
Dall'equazione che abbiamo ricavato dall'equilibrio sull'asse X
$T_1=\frac{T_2cos(45°)}{cos(60°)}$
Ora che abbiamo ricavato $T_2$ possiamo inserire il valore numerico e ricavare anche $T_1$
$T_1=0,021N$
- Esercizio 5 (piano inclinato)
Per prima cosa disegniamo tutte le forze, considerando anche l'attrito
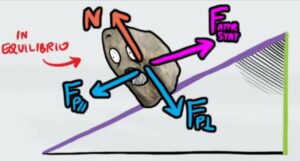
Scriviamo le equazioni che permettono l'equilibrio su entrambi gli assi (dove $F_a$ è la forza di attrito)
EQUILIBRIO ASSE Y → $N-P_y=0$
EQUILIBRIO ASSE X → $F_a+T-P_x=0$
Calcoliamo le due componenti del peso (ricordando che nel piano inclinato la componente Y si calcola con il coseno e la componente X con il seno)
$P_x=mgsin(10°)=8,52N$
$P_y=mgcos(10°)=48,3N$
RICAVARE L'ATTRITO
Dall'equilibrio sull'asse y possiamo ricavare la reazione vincolare.
$N=P_x=48,3N$
Ora che abbiamo la reazione vincolare possiamo ricavare la forza di attrito statico massima dalla formula
$F_a=μ_sN=4,84N$
RICAVARE LA TENSIONE
Ora abbiamo tutte le forze tranne la tensione che si può ricavare dall'equilibrio sull'asse X
$F_a+T-P_x=0$
$T=P_x-F_a=3,68N$
- Esercizio 6 (piano inclinato)
Per prima cosa disegniamo le 4 forze principali in ognuno delle due casse; la reazione vincolare, le due componenti delle forze peso e la tensione del filo.
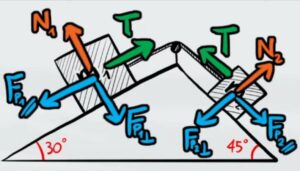
Adesso le due forze di attrito dei due corpi dipendono in base a come si evolve il problema. Infatti ci sono due casi: il primo in cui la cassa 1 vince sulla cassa 2 e scivola sul piano inclinato trascinando con se la cassa 2 o viceversa.

Per poterlo capire dobbiamo capire quale delle due forze prevale sull'altra. Dal grafico delle forze possiamo vedere che l'unica forza che tende a far scivolare le due casse dal piano è la componente X del peso.
Quindi per poter capire quale forza vince sull'altra basta calcolare le forze peso X e confrontare i risultati
MASSA 1 $P_x=m_1gsin(30°)=49N$
MASSA 2 $P_x=m_2gsin(45°)=42N$
Quindi la cassa 1 vince sulla cassa 2, quindi l'attrito deve bilanciare il peso della cassa 1
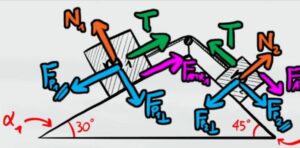
EQUILIBRIO
Ora possiamo scrivere le condizioni di equilibrio sui due assi. Dove $F_A$ sono le forze di attrito.
Le forze rivolte verso sinistra le mettiamo con segno positivo e quelle rivolte verso destra con segno negativo.
EQUILIBRIO ASSE X → $P_{1x}-F_{A1}-T+T-P_{2x}-F_{A2}=0$
$P_{1x}-F_{A1}-P{2x}-F_{A2}=0$
L'equilibrio sull'asse X descrive l'intero sistema di 2 casse mentre l'equilibrio sull'asse Y considera le singole casse in quanto il movimento sull'asse Y di una non influenza quello dell'altro. L'equilibrio sull'asse Y delle due casse risulta essere:
$P_{1y}-N_1=0$
$P_{2y}-N_2=0$
Dall'equilibrio sull'asse Y ricaviamo le due reazioni vincolari
$N_1=m_1gcos(30°)=85N$
$N_2=m_2gcos(45°)=41,6N$
Avendo le reazioni vincolari possiamo riscrivere le due forze di attrito minime come
$F_{A1}=N_1μ_s$
$F_{A2}=N_2μ_s$
Possiamo inserire queste due forze di attrito nell'equilibrio sull'asse X
$P{1x}-N_1μ_s-P{2x}-N_2μ_s=0$
Di questa equazione abbiamo tutte le incognite tranne il coefficiente di attrito statico, che possiamo ricavare risolvendo l'equazione. Per prima cosa raccogliamo il coefficiente
$-μ_s(N_1+N_2)+P{1x}-P{2x}=0$
$-μ_s(N_1+N_2)=-P{1x}+P{2x}=0$
$μ_s(N_1+N_2)=P{1x}-P{2x}=0$
Risolvendo otteniamo
$μ_s=\frac{P_{1x}-P_{2x}}{N_1+N_2}$
Sostituendo tutti i termini con quello che abbiamo ricavato otteniamo questa espressione:
$μ_S=\frac{m_1gsin(30°)-m_2gsin(45°)}{m_1gcos(30°)+m_2gcos(45°)}$
Sia al numeratore e al denominatore si può raccogliere g e semplificarla
$μ_S=\frac{m_1sin(30°)-m_2sin(45°)}{m_1cos(30°)+m_2cos(45°)}$
- Esercizio 7 (carrucola)
Per prima cosa calcoliamo i pesi delle due masse sulla carrucola ($m_1=5kg$ e $m_2=3kg$)
$P_1=m_1g=49N$
$P_2=m_2g=29,4N$
Dal secondo principio della dinamica abbiamo che la somma di tutte le forze che agiscono su un corpo è $ma$. Sulle due masse agiscono due forze; la forza peso e la tensione della carrucola
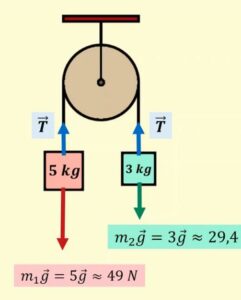
Possiamo dunque scrivere due equazioni, una per il primo corpo e l'altra per il secondo (le forze verso l'alto hanno segno positivo, mentre quelle verso il basso segno negativo)
MASSA 1 → $T-P_1=-m_1a$
MASSA 2 → $T-P_2=m_2a$
I due corpi sono collegati tra di loro da una fune quindi hanno la stessa accelerazione $a$. L0unica differenza è che la massa 1 ha un peso maggiore rispetto alla massa 2, quindi cade con accelerazione verso il basso (per questo ha accelerazione negativa) e nel frattempo la massa 2 sale con accelerazione rivolta verso l'alto (accelerazione positiva).
Sostituiamo intanto i pesi delle due masse con $mg$
MASSA 1 → $T-m_1g=-m_1a$
MASSA 2 → $T-m_2g=m_2a$
RICAVARE L'ACCELERAZIONE
Dalla prima equazione ricaviamo la tensione della fune attaccata alla carrucola
$T=m_1g-m_1a$
E la sostituiamo nella tensione dell'equazione della massa 2
$m_1g-m_1a-m_2g=m_2a$
E ora risolviamo per $a$
$m_1g-m_1a-m_2g-m_2a=0$
Raccogliamo $a$
$-a(m_1+m_2)+m_1g-m_2g=0$
$-a(m_1+m_2)=m_2g-m_1g$
$a=-\frac{m_2g-m_1g}{m_1+m_2}=2,45m/s^2$
RICAVARE LA TENSIONE
Ora possiamo riprendere l'equazione che abbiamo ricavato prima per la tensione
$T=m_1g-m_1a$
E sostituire l'accelerazione con il valore che abbiamo trovato ottenendo
$T=36,75N$
