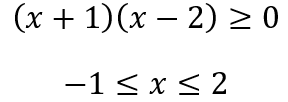Lo studio del segno serve a capire per quali valori della variabile una funzione è positiva, negativa o nulla.
Per prima cosa si pone la funzione scelta maggiore o uguale a 0
![]()
Lo studio del segno si può differenziare in tre passi:
- Scrivere le serie di disequazioni per cui la funzione è positiva
- Risolvere le disequazioni
- Scrivere i risultati dei segni sul grafico
- Fare il prodotto tra i segni
Poi bisogna scrivere una serie di disequazioni per trovare i valori di x per cui la funzione è positiva. Da qui dobbiamo differenziare i casi:
- Prodotto di funzioni
Come ad esempio
![]()
Nei prodotti dobbiamo considerare i singoli polinomi (x+1) e (x-2). Il prodotto di due polinomi è positivo solo se sono entrambi positivi o entrambi negativi
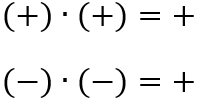
Quindi avremo due serie di disequazioni, una in cui sono entrambi positivi
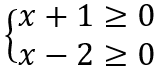
E una in cui sono entrambi negativi
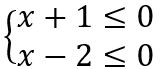
Risolvendole abbiamo
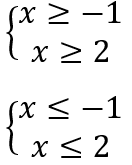
Risolvendo i due sistemi di disequazioni otteniamo
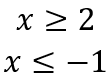
A questo punto disegniamo una retta che contenga questi due numeri risultati (-1 e 2)

Come primo risultato abbiamo ottenuto $x\geq 2$ mettiamo un segno + per i numeri maggiori o uguali a 2 e - per tutti i numeri minori di 2
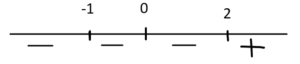
Come secondo risultato invece abbiamo ottenuto $x\leq -1$ quindi mettiamo un segno + per tutti i numeri minori o uguali a 1 e un segno - per tutti i numeri maggiori di 1
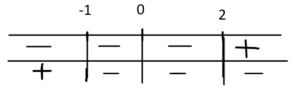
Come passaggio finale moltiplichiamo tra loro i segni in colonna (-)*(+), (-)*(-) ecc... ottenendo
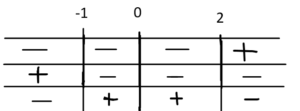
Quindi, in conclusione, abbiamo che dal grafico finale possiamo vedere che la funzione è positiva (segno +) per x compresa tra -1 e 2 e negativa per tutto il resto