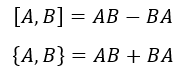Lo spazio di Hilbert è il campo di esistenza di una particella oltre il quale essa cesserebbe di esistere, cioè è una regione di spazio in cui la particella si trova e abbiamo che nel campo di Hilbert vale la seguente relazione per la funzione d’onda:

In questo spazio ogni vettore della particella è rappresentato da un ket (vedi autovettori e autovalori)
![]()
Un ket moltiplicato per un bra dello stesso vettore dando come risultato 1
![]()
a è un ket dello spazio di Hilbert mentre A è un operatore definito in genere come una derivata o una matrice. Tra di loro gli operatori spesso non commutano
![]()
L’operatore di commutazione e di anticommutazione sono i seguenti: