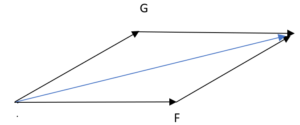
Siccome F e G formano tra loro un angolo di 30° dobbiamo sommare le componenti x (con il coseno) e y (con il seno)
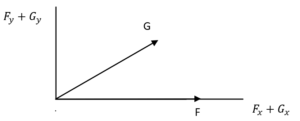
$ F_x=|F|cos(30°)=5,2 F_y=|F|sin(30°)=3 $
$ G_x=|G|cos(30°)=3,5 G_y=|G|sin(30°)=2 $
Per ottenere le componenti del vettore risultante basta sommare tra loro le x e le y (chiamiamo R il vettore risultante)
$ R_x=G_x+F_x=3,5+5,2=8,7 $
$R_y=F_y+G_y=3+2=5$
A questo punto per trovare il modulo del vettore risultante R basta fare il teorema di Pitagora delle componenti
$|R|=\sqrt{R_x^2+R_y^2}=\sqrt{8,7^2+5^2}=10,03$
Il metodo punta-coda consiste nel traslare (cioè spostare) la punta di uno dei due vettori in modo tale che tocchi la coda dell'altro vettore.
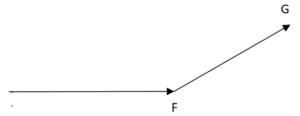
In questo modo il vettore risultante risulta essere il segmento che unisce la coda di F con la punta di G
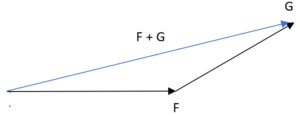
Il metodo del parallelogramma consiste nel costruire un parallelogramma facendo partire da ognuno dei due vettori un segmento parallelo all'altro vettore
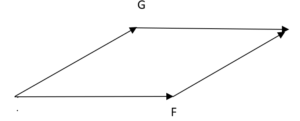
Ora basta tracciare, dall'intersezione di F e G, la diagonale del parallelogramma per trovare il vettore risultante