Clicca qui per vedere la pagina degli esercizi
- Esercizio 1
a) Se A e B sono paralleli semplicemente si sommano i moduli$ |A|+|B|=3+4=7 $
b)Se A e B sono perpendicolari (cioè formano un angolo di 90° tra loro) il modulo del vettore somma si trova facendo il teorema di Pitagora
$ \sqrt{|A|^2+|B|^2}=\sqrt{9+16}=\sqrt{25}=5 $
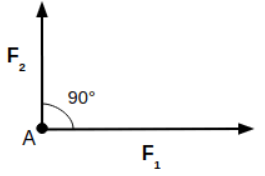
c)Se A e B hanno verso opposto la loro somma equivale ad una sottrazione
$\vec{A}+(-\vec{B})=\vec{A}-\vec{B}=3-4=-1 $
Di conseguenza il verso del vettore risultante sarà lo stesso del vettore di modulo maggiore tra i due (in questo caso B)
Esercizio 2
a) Siccome i due vettori sono perpendicolari, la loro somma si svolge con il teorema di Pitagora
$|\vec{M}+\vec{N}|=\sqrt{|M|^2+|N|^2}=\sqrt{100+144}=\sqrt{244} $
IMMAGINE
b)Il modulo del vettore somma è un numero sempre positivo ed è uguale a quello ottenuto nella somma
$ |\vec{M}-\vec{N}|=\sqrt{|M|^2+|N|^2}=\sqrt{244} $
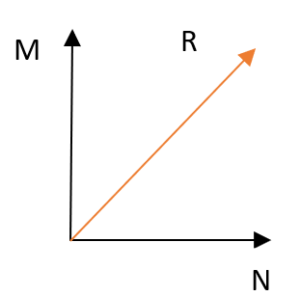
L'unica differenza è che in b) il vettore somma ha verso e direzione opposta rispetto al vettore somma in a)
c) In questo caso nel modulo semplicemente M viene raddoppiato
$ |2\vec{M}-\vec{N}|=\sqrt{|2M|^2+|N|^2}=\sqrt{400+144}=\sqrt{544} $
- Esercizio 3
Siccome F e G formano tra loro un angolo di 30° dobbiamo sommare le componenti x (con il coseno) e y (con il seno)
$ F_x=|F|cos(30°)=5,2 F_y=|F|sin(30°)=3 $
$ G_x=|G|cos(30°)=3,5 G_y=|G|sin(30°)=2 $
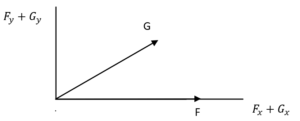
Per ottenere le componenti del vettore risultante basta sommare tra loro le x e le y (chiamiamo R il vettore risultante)
$ R_x=G_x+F_x=3,5+5,2=8,7 $
$R_y=F_y+G_y=3+2=5$
A questo punto per trovare il modulo del vettore risultante R basta fare il teorema di Pitagora delle componenti
$|R|=\sqrt{R_x^2+R_y^2}=\sqrt{8,7^2+5^2}=10,03$
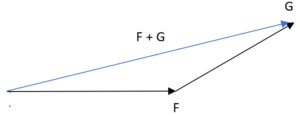
Il metodo punta-coda consiste nel traslare (cioè spostare) la punta di uno dei due vettori in modo tale che tocchi la coda dell'altro vettore.
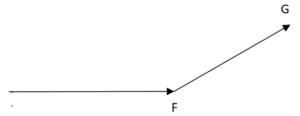
In questo modo il vettore risultante risulta essere il segmento che unisce la coda di F con la punta di G
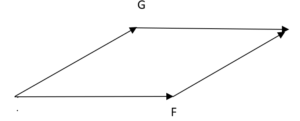
Il metodo del parallelogramma consiste nel costruire un parallelogramma facendo partire da ognuno dei due vettori un segmento parallelo all'altro vettore
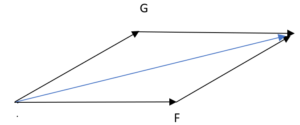
Ora basta tracciare, dall'intersezione di F e G, la diagonale del parallelogramma per trovare il vettore risultante
4)
a) Siccome le componenti x e y del vettore sono tutte e due positive, significa che il vettore si trova nel quadrante positivo del piano cartesiano.
b) Il modulo del vettore si trova facendo il teorema di Pitagora delle sue componenti
$ r=\sqrt{r_x^2+r_y^2}=\sqrt{5^2+7^2}=\sqrt{74} $
c)L'angolo di inclinazione lo si può ricavare usando le formule trigonometriche applicate ad un triangolo rettangolo considerando il vettore come ipotenusa e le sue componenti i cateti. In questo modo abbiamo che:
$ r_y=r_xtan(a) $
Da qui ricaviamo l'angolo a
$ a=tan^{-1}(\frac{r_y}{r_x})=54° $