PAGINA DI ESERCIZI: QUANTITA' DI MOTO
- Esercizio 1
Il ragazzo, siccome si trova sopra lo skateboard, si muove alla sua stessa velocità, quindi la quantità di moto totale del sistema skateboard+ragazzo è data dalla somma delle due quantità di moto

$p_{tot}=p_r+p_s$
Dove $p_r$ è la quantità di moto del ragazzo e $p_s$ quella dello skatebord. Per calcolarle usiamo la formula della quantità di moto
$p_r=m_rv$
$p_s=m_sv$
Quindi la quantità di moto totale diventa
$p_{tot}=m_rv+m_sv$
Da qui possiamo ricavare la massa dello skateboard ($m_s$)
$m_sv=p_{tot}-m_rv$
$m_s=\frac{p_{tot}-m_rv}{v}$
Sostituendo con i valori numerici otteniamo
$m_s=3kg$
- Esercizio 2
Come indicato nel problema, i due ballerini partono da fermi ($v=0$) per cui le quantità di moto inziali sono:
$p_{1i}=m_1\cdot 0=0$
$p_{2i}=m_2\cdot 0=0$
La quantità di moto inziale sarà quindi la somma di tutte le quantità di moto dei corpi all'inizio
$p_{tot_i}=0$
Successivamente i due ballerini iniziano a muoversi a velocità $v_1$ e $v_2$
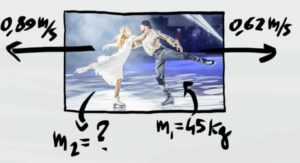
Quindi le quantità di moto finali sono
$p_{1f}=m_1v_1$
$p_{2f}=m_2v_2$
La quantità di moto totale finale è data dalla somma delle due quantità di moto finali.
$p_{tot_f}=m_1v_1+m_2v_2$
CONSERVAZIONE
Dalla conservazione della quantità di moto:
$p_{tot_f}=p_{tot_i}$
Sostituendo i valori ricavati per le due quantità di moto totali otteniamo
$m_1v_1+m_2v_2=0$
Da qui possiamo ricavare ciò che il problema ci aveva chiesto, ovvero la massa del ballerino 2
$m_2v_2=-m_1v_1$
$m_2=-\frac{m_1v_1}{v_2}$
Il segni meno indica solamente che i due corpi si muovono in direzione opposta, ma questo si annulla considerando $v_2$ negativa (dato che è opposta a $v_1$)
$m_2=\frac{m_1v_1}{v_2}=31,3kg$
- Esercizio 3
TROVARE L'EQUAZIONE
Nel problema viene richiesto la distanza tra l'astronauta e la navicella, quindi dobbiamo trovare un equazione del moto che consideri la distanza dell'astronauta. Questa formula è proprio quella della velocità
$v_a=\frac{Δd}{Δt}$
Per ricavare la velocità dell'astronauta dobbiamo utilizzare la conservazione della quantità di moto:
QUANTITA' DI MOTO
L'astronauta e il satellite partono da fermi, quindi le quantità di moto inziali sono a velocità nulla
$p_{a_i}=m_a\cdot 0=0$
$p_{s_i}=m_s\cdot 0=0$
La quantità di moto totale iniziale totale del sistema è
$p_{tot_i}=0+0=0$
Dopo l'urto tra l'astronauta e il satellite, i due corpi si muovono. Quindi le quantità di moto finali saranno date dalla velocità dei due corpi dopo l'urto
$p_{a_f}=m_av_a$
$p_{s_f}=m_sv_s$
Quindi la quantità di moto finale totale sarà la somma delle due quantità di moto finali
$p_{tot_f}=m_av_a+m_sv_s$
CONSERVAZIONE DELLA QUANTITA' DI MOTO
Dalla formula della conservazione della quantità di moto:
$p_{tot_i}=p_{tot_f}$
Possiamo sostituire le due quantità di moto totali con quelle che abbiamo ricavato
$0=m_av_a+m_sv_s$
Di questa equazione l'unica variabile è la velocità dell'astronauta che può essere ricavata
$m_av_a=-m_sv_s$
$v_a=-\frac{m_sv_s}{m_a}=-1,52m/s$
Il segno meno indica solamente che l'astronauta si muove in direzione opposta rispetto al satellite, ma a noi interessa solamente il modulo della velocità
$v_a=1,52m/s$
RICAVARE LA DISTANZA
Dalla formula del moto mostrata all'inizio
$v_a=\frac{Δd}{Δt}$
Da qui possiamo ricavare la distanza tra la navicella (punto di arrivo) e l'astronauta all'inizio (posizione inziale)
$Δd=v_aΔt=11,4m/s$
- Esercizio 4
Per poter risolvere l'esercizio dobbiamo visualizzare il problema, il cannone spara una palla verso destra ad un angolo di 45° e dopo il colpo rincula andando indietro. Quindi la rappresentazione sul piano cartesiano è questa:
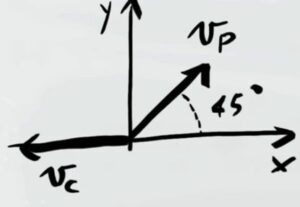
Dove $v_c$ è la velocità del cannone e $v_p$ la velocità della palla.
Siccome $v_p$ forma un angolo di 45° con l'asse X, possiamo scomporre la velocità della palla nelle sue due componenti
$v_{p_x}=v_pcos(45°)=90,5m/s$
$v_{p_y}=v_psin(45°)=90,5m/s
(NOTA: di queste due componenti della velocità della palla, considereremo solo la componente X perché è lo stesso asse su cui si muove anche il cannone, cioè da destra verso sinistra)
QUANTITA' DI MOTO
Il cannone, prima dello sparo, rimane fermo. Quindi la sua quantità di moto inziale è a velocità nulla
$p_{c_i}=m_c\cdot 0=0$
La stessa cosa avviene con la palla, che prima lo sparo è ferma dentro il cannone
$p_{p_i}=m_p\cdot 0=0$
Quindi la quantità di moto inziale totale è la somma delle due quantità di moto iniziali
$p_{tot_i}=0+0=0$
Successivamente allo sparo, a causa del rinculo, si muove a velocità $v_c$. La sua quantità di moto finale, dunque, sarà data da
$p_{c_f}=m_cv_c$
Stessa cosa per la palla che dopo lo sparo assume velocità $v_p$. Quindi la quantità di moto finale sull'asse X della palla sarà
$p_{px_f}=m_pv_pcos(45°)$
Quindi la quantità di moto finale del sistema sull'asse X sarà data dalla somma delle due quantità di moto finali:
$p_{tot_f}=m_cv_c+m_pv_pcos(45°)$
CONSERVAZIONE DELLA QUANTITA' DI MOTO
Dalla formula della conservazione della quantità di moto, abbiamo che la quantità di moto totale inziale è uguale a quella totale finale
$p_{tot_f}=p{tot_i}$
Sostituendo con i valori ricavati otteniamo
$m_cv_c+m_pv_pcos(45°)=0$
Da qui possiamo ricavare la massa del cannone $m_c$ risolvendo questa semplice equazione
$m_cv_c=-m_pv_pcos(45°)$
$m_c=-\frac{m_pv_pcos(45°)}{v_c}$
Siccome la velocità del cannone è opposta alla velocità della palla, $v_c$ risulta negativa. Per cui il segno meno della velocità si semplifica con il segno meno presente davanti alla frazione
$m_c=\frac{m_pv_pcos(45°)}{v_c}=693kg$
- Esercizio 5
Dai dati abbiamo le velocità inziali prima dell'urto ($v_{A_i}=5m/s$ e $v_{B_i}$) e le velocità finali dopo l'urto ($v_{A_f}=1,5m/s$ e $v_{B_f}=4m/s$) con la velocità inziale del corpo B come incognita.
Per ricavare l'incognita dobbiamo per prima cosa calcolare le quantità di moto inziali
$p_{A_i}=m_Av_{A_i}$
$p_{B_i}=m_Bv_{B_i}$
E le quantità di moto finali
$p_{A_f}=m_Av_{A_f}$
$p_{B_f}=m_Bv_{B_f}$
In questo modo possiamo calcolare la quantità di moto totale inziale facendo la somma delle quantità di moto inziali e la quantità di moto totale finale facendo la somma delle quantità di moto finali
$p_{tot_i}=m_Av_{A_i}+m_Bv_{B_i}$
$p_{tot_f}=m_Av_{A_f}+m_Bv_{B_f}$
Dalla formula della conservazione della quantità di moto abbiamo che la quantità di moto totale inziale è uguale a quella totale finale.
$p_{tot_i}=p_{tot_f}$
Quindi
$m_Av_{A_i}+m_Bv_{B_i}=m_Av_{A_f}+m_Bv_{B_f}$
L'unica incognita è la velocità inziale del corpo B ($v_{B_i}$) che si può ricavare risolvendo l'equazione
$m_Bv_{B_i}=m_Av_{A_f}+m_Bv_{B_f}-m_Av_{A_i}$
$v_{B_i}=\frac{m_Av_{A_f}+m_Bv_{B_f}-m_Av_{A_i}}{m_B}$
Svolgendo i calcoli si ottiene
$v_{B_i}=-3m/s$
Il segno meno indica che prima dell'urto il corpo B stava andando in direzione opposta rispetto al corpo A. Quindi si sono scontrati durante il percorso.
- Esercizio 6
Le palline 2 e 3 partono da ferme, quindi hanno velocità inziale nulla mentre la pallina 1 ha velocità inziale di $v_{1i}=10m/s$.
Sapendo le masse delle 3 palle possiamo calcolare le quantità di moto inziali
$p_{1i}=2mv_{1i}$
$p_{2i}=m\cdot 0=0$
$p_{3i}=m\cdot 0=0$
Facendo la somma otteniamo la quantità di moto inziale totale del sistema
$p_{tot_i}=mv_{1i}+0+0=2mv_{1i}$
Successivamente il problema non da informazioni sulle velocità finali delle 3 palline, quindi possiamo supporre che ogni pallina trasferisce tutta la sua quantità di moto alla pallina successiva. Cioè la pallina 1 dopo aver urtato la pallina 2 si ferma e mette in moto la pallina 2 e così via per la pallina 3.
Alla fine l'unica pallina che alla fine si muove è proprio la pallina 3 con velocità $v_{3f}$
Quindi le palline 2 e 3 hanno velocità nulla, dunque le quantità di moto finali sono:
$p_{1f}=2m\cdot 0=0$
$p_{2f}=m\cdot 0=0$
$p_{3f}=mv_{3f}$
La somma di queste tre quantità di moto finali è la quantità di moto finale totale del sistema
$p_{tot_f}=0+0+mv_{3f}=mv_{3f}$
CONSERVAZIONE DELLA QUANTITA' DI MOTO
Dalla formula della conservazione della quantità di moto:
$p_{tot_i}=p_{tot_f}$
Sostituendo con le due quantità di moto finali ricavate otteniamo:
$2mv_{1i}=mv_{3f}$
Da qui possiamo ricavare la velocità finale della terza palla
$v_{3f}=\frac{2mv_{1i}}{m}=2v_{1i}$
Svolgendo i calcoli ricaviamo
$v_{3f}=20m/s$
- Esercizio 7
L'urto è completamente elastico con due incognite, quindi dobbiamo considerare la conservazione della quantità di moto e dell'energia cinetica per ricavarle entrambe.
QUANTITA' DI MOTO
Per prima cosa dobbiamo calcolare le quantità di moto inziali e finali dei due corpi
La macchina parte da ferma, per cui la sua quantità di moto inziale è a velocità nulla
$p_{A_i}=m_A\cdot 0=0$
Mentre il furgone già in partenza era in movimento con velocità $v_{F_i}$ e quantità di moto data da
$p_{F_i}=m_Fv_{F_i}$
Quindi la quantità di moto totale inziale del sistema è la somma di queste due
$p_{tot_i}=0+m_Fv_{F_i}=m_Fv_{F_i}$
Alla fine invece i due corpi si muovono con velocità incognite $v_{A_f}$ e $v_{F,f}$ con cui possiamo scrivere le due quantità di moto finali
$p_{A_f}=m_Av_{A_f}$
$p_{F_f}=m_Fv_{F_f}$
Quindi la quantità di moto finale totale del sistema
$p_{tot_f}=m_Av_{A_f}+m_Fv_{F_f}$
Dalla conservazione della quantità di moto abbiamo che
$p_{tot_i}=p_{tot_f}$
Sostituendo con i valori ricavati
$m_Fv_{F_i}=m_Av_{A_f}+m_Fv_{F_f}$
Però per ricavare due incognite ci servono una serie di due equazioni, quindi ora dobbiamo ricavare anche la conservazione dell'energia cinetica.
CONSERVAZIONE DELL'ENERGIA CINETICA
Le energie cinetiche inziali dei due corpi sono (ricordando che l'auto parte da ferma):
$E_{A_i}=\frac{1}{2}m_A\cdot 0=0$
$E_{F_i}=\frac{1}{2}m_Fv_{F_i}^2$
E le energie cinetiche finali
$E_{A_f}=\frac{1}{2}m_Av_{A_f}^2$
$E_{F_f}=\frac{1}{2}m_Fv_{F_f}^2$
Facciamo le somme delle energia cinetiche inziali e le energie cinetiche finali
$E_{tot_i}=\frac{1}{2}m_Fv_{F_i}^2$
$E_{tot_f}=\frac{1}{2}m_Av_{A_f}^2+\frac{1}{2}m_Fv_{F_f}^2$
Dalla conservazione dell'energia cinetica abbiamo che l'energia cinetica totale finale è uguale a quella totale inziale, quindi possiamo scrivere un uguaglianza tra le due energie
$\frac{1}{2}m_Fv_{F_i}^2=\frac{1}{2}m_Av_{A_f}^2+\frac{1}{2}m_Fv_{F_f}^2$
Da qui in poi sono solo passaggi matematici
Per poter trovare le due variabili dobbiamo mettere a sistema la conservazione della quantità di moto e quella dell'energia cinetica che abbiamo appena ricavato
$m_Fv_{F_i}=m_Av_{A_f}+m_Fv_{F_f}$
$\frac{1}{2}m_Fv_{F_i}^2=\frac{1}{2}m_Av_{A_f}^2+\frac{1}{2}m_Fv_{F_f}^2$
Dalla conservazione della quantità di moto (la prima equazione) ricaviamo una delle due velocità finali, per scelta ricaviamo la velocità finale del furgone $v_{F_f}$
$m_Fv_{F_f}=m_Fv_{F_i}-m_Av_{A_f}$
$v_{F_f}=\frac{m_Fv_{F_i}-m_Av_{A_f}}{m_F}$
E questa velocità la sostituiamo all'interno della conservazione dell'energia cinetica al posto della velocità finale del furgone
$\frac{1}{2}m_Fv_{F_i}^2=\frac{1}{2}m_Av_{A_f}^2+\frac{1}{2}m_F\cdot (\frac{m_Fv_{F_i}-m_Av_{A_f}}{m_F})^2$
Le due masse del furgone al numeratore e al denominatore si semplificano
$\frac{1}{2}m_Fv_{F_i}^2=\frac{1}{2}m_Av_{A_f}^2+\frac{1}{2}\cdot \frac{(m_Fv_{F_i}-m_Av_{A_f})^2}{m_F}$
Moltiplichiamo tutti i membri dell'equazione per $m_F$ per cancellare il denominatore
$\frac{1}{2}m_{F}^2v_{F_i}^2=\frac{1}{2}m_Fm_Av_{A_f}^2+$
$\frac{1}{2}\cdot (m_Fv_{F_i}-m_Av_{A_f})^2$
Sviluppiamo il quadrato di binomio presente a destra dell'equazione
$\frac{1}{2}m_{F}^2v_{F_i}^2=\frac{1}{2}m_Fm_Av_{A_f}^2+$
$\frac{1}{2}\cdot (m_{F}^2v_{F_i}^2+m_{A}^2v_{A_f}^2-2m_Fm_Av_{F}v_{A})$
Sviluppando i calcoli diventa
$\frac{1}{2}m_{F}^2v_{F_i}^2=\frac{1}{2}m_Fm_Av_{A_f}^2+$
$\frac{1}{2}m_{F}^2v_{F_i}^2+\frac{1}{2}m_{A}^2v_{A_f}^2-m_Fm_Av_{F}v_{A}$
Da qui raccogliamo tutti i termini che contengono $v_{A_f}^2$
$v_{A_f}^2(\frac{1}{2}m_Fm_A+\frac{1}{2}m_{A}^2) +\frac{1}{2}m_{F}^2v_{F_i}^2-m_Fm_Av_{F}v_{A}$
$=\frac{1}{2}m_{F}^2v_{F_i}^2$
Portiamo tutti i termini a sinistra dell'equazione e ordiniamo per $v_{A_F}$
$v_{A_f}^2(\frac{1}{2}m_Fm_A+\frac{1}{2}m_{A}^2) -m_Fm_Av_{F}v_{A}+\frac{1}{2}m_{F}^2v_{F_i}^2$
$-\frac{1}{2}m_{F}^2v_{F_i}^2=0$
Qua si può vedere che l'equazione per trovare $v_{A_f}$ è una equazione di secondo grado. Quindi dobbiamo risolverla con la formula risolutiva (considerando solamente la soluzione positiva con il + davanti al delta)
$v_{A_f}=\frac{m_Fm_Av_{F}+\sqrt{(m_Fm_Av_{F})^2-4(\frac{1}{2}m_Fm_A+\frac{1}{2}m_{A}^2)(\frac{1}{2}m_{F}^2v_{F_i}^2-\frac{1}{2}m_{F}^2v_{F_i}^2)}}{m_Fm_A+m_{A}^2}$
Svolgendo i calcoli otteniamo
$v_{A_f}=21,7m/s$
Sostituendo questa velocità nella formula che abbiamo utilizzato per sostituire la velocità finale del furgone
$v_{F_f}=\frac{m_Fv_{F_i}-m_Av_{A_f}}{m_F}$
Ottenendo
$v_{F_f}=6,25m/s$
- Esercizio 8
CONSERVAZIONE DELLA QUANTITA' DI MOTO
Il problema ci chiede la velocità del sistema delle due palline, quindi all'inizio dobbiamo considerare la quantità di moto delle due palline come un'unica quantità di moto totale
$p_{tot_f}=m_{tot}v_{tot}$
Dove la massa totale $m_{tot}$ è semplicemente la massa delle due palline
$p_{tot_f}=(m_1+m_2)v_{tot}$
Questa grandezza rappresenta la quantità di moto totale del sistema dopo l'urto, cioè rappresenta la quantità di moto totale finale
Le quantità di moto inziali delle due palline si possono calcolare conoscendo le due masse ($m_1$ e $m_2$) e le due velocità ($v_1$ e $v_2$)
$p_{1i}=m_1v_1$
$p_{2i}=m_2v_2$
Quindi la quantità di moto totale inziale sarà la somma di queste due
$p_{tot_i}=m_1v_1+m_2v_2$
Quindi per la conservazione della quantità di moto le due quantità di moto totali sono uguali
$p_{tot_i}=p_{tot_f}$
$m_1v_1+m_2v_2=m_{tot}v_{tot}$
RICAVARE LA VELOCITA' TOTALE
Dopo l'urto si crea un angolo tra le due palline
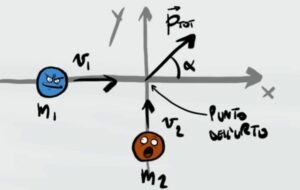
Quindi possiamo scomporre la quantità di moto totale nelle sue due componenti.
$p_{tot_xf}=(m_1+m_2)v_{tot}cos(α)$
$p_{tot_yf}=(m_1+m_2)v_{tot}sin(α)$
La conservazione della quantità di moto può anch'essa essere divisa nelle due componenti
$p_{tot_xi}=p_{tot_xf}$
$p_{tot_yi}=p_{tot_yf}$
Inizialmente la pallina 1 si muove solo sull'asse X mentre la pallina 2 solo sull'asse Y. Quindi la pallina 1 rappresenta la quantità di moto sull'asse X mentre la pallina 2 la quantità di moto sull'asse Y
$m_1v_1=p_{tot_xf}$
$m_2v_2=p_{tot_yf}$
Sostituendo le quantità di moto finali con le due componenti otteniamo
$m_1v_1=(m_1+m_2)v_{tot}cos(α)$
$m_2v_2=(m_1+m_2)v_{tot}sin(α)$
In queste equazioni l'unica quantità che viene scomposta nelle sue due componenti è la velocità totale
$v_{tot_x}=v_{tot}cos(α)$
$v_{tot_y}=v_{tot}sin(α)$
Quindi dalle due equazioni possiamo ricavare le due componenti della velocità totale
$v_{tot_x}=\frac{m_1v_1}{m_1+m_2}$
$v_{tot_y}=\frac{m_2v_2}{m_1+m_2}$
Per ricavare un vettore dalle sue componenti dobbiamo applicare il teorema di Pitagora alle due componenti
$v_{tot}=\sqrt{(\frac{m_1v_1}{m_1+m_2})^2+(\frac{m_2v_2}{m_1+m_2})^2}$
Dall'espressione che abbiamo trovato possiamo raccogliere $(m_1+m_2)^2$ e portarlo fuori dalla radice
$v_{tot}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}$
ANGOLO α
Dalla formula della componente X della velocità finale
$v_{tot_x}=v_{tot}cos(α)$
Possiamo sostituire $v_{tot_x}$ e $v_{tot}$ con le due espressioni che abbiamo trovato prima
$v_{tot_x}=\frac{m_1v_1}{m_1+m_2}$
$v_{tot}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}$
Sostituendo nell'espressione otteniamo
$\frac{m_1v_1}{m_1+m_2}=\frac{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}{m_1+m_2}cos(α)$
Da qui possiamo ricavare l'angolo α
$cos(α)=\frac{m_1v_1}{m_1+m_2}\cdot \frac{m_1+m_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}$
Semplificando otteniamo
$cos(α)=\frac{m_1v_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}}$
E applicando l'arcocoseno ad entrambi i membri otteniamo l'angolo α
$α=arccos(\frac{m_1v_2}{\sqrt{(m_1v_1)^2+(m_2v_2)^2}})$
