PAGINA DI TEORIA: QUANTITA' DI MOTO
La quantità di moto è una grandezza vettoriale descritta dal prodotto di massa per velocità di un corpo
$p=mv$
Ed è una grandezza particolarmente utile quando si trattano problemi riguardanti gli urti o più corpi che si muovono.
Quando si trattano più corpi che urtano tra di loro in un sistema isolato (cioè che non interagiscono con altri corpi esterni) bisogna considerare sempre la conservazione della quantità di moto
$Δ\vec{p}_{tot}=0$
Cioè la somma delle quantità di moto inziali è uguale alla somma delle quantità di moto finali
$\vec{p}_{1i}+\vec{p}_{2i}...=\vec{p}_{1f}+\vec{p}_{2f}...$
Dove ogni quantità di moto è associata ad uno dei corpi considerati.
TIPI DI URTI
Gli urti possono essere:
- Elastici (due corpi si urtano e poi rimbalzano): avviene la conservazione della quantità di moto e dell'energia cinetica.
$Δ\vec{p}_{tot}=0$
$ΔE_{tot}=0$
- Anelastici (due corpi si urtano e rimangono attaccati o si deformano): avviene solamente la conservazione della quantità di moto
$Δ\vec{p}_{tot}=0$
- Esercizio 1
Un ragazzo di massa $m=60kg$ su uno skateboard va ad una velocità $v=5m/s$. La quantità di moto del sistema (ragazzo+skateboard) è $p_{tot}=320kg\cdot m/s$. Calcola la massa dello skateboard.

- Esercizio 2
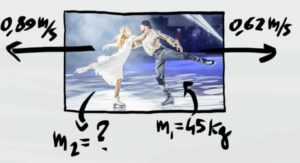
Due ballerini danzano insieme su una pista di pattinaggio. Partendo da fermi, cominciano a muoversi con una velocità di $v_1=0,5m/s$ e $v_2=0,6m/s$. Il primo ballerino ha una massa di $m_1=45kg$. Calcola la massa del secondo ballerino.
- Esercizio 3
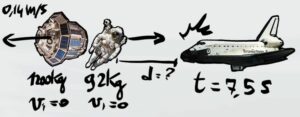
Un astronauta di massa $m_A=92kg$ e un satellite di massa $m_S=1000kg$ sono inizialmente fermi rispetto ad una navicella. Ad un certo punto l'astronauta urta il satellite che acquisisce velocità $v_S=0,14m/s$. Dopo 7,5 secondi l'astronauta urta la navicella.
Qual era la distanza inziale tra l'astronauta e la navicella?
- Esercizio 4
Da un cannone viene sparata una palla di massa $m_p=24,5kg$ ad una velocità $v_p=128m/s$. Il colpo viene sparato ad un angolazione di 45° rispetto al terreno e dopo il colpo il cannone rincula indietro ad una velocità $v_c=3,2m/s$. Calcola la massa del cannone

- Esercizio 5
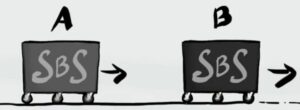
Un carrello A di massa $m_A=1kg$ va ad una velocità $v_A=5m/s$ e nel suo tragitto urta un carrello B di massa $m_B=0,5kg$. Dopo l'urto i due carrelli vanno a velocità $v_A=1,5m/s$ e $v_B=4m/s$.
Qual era la velocità di B prima dell'urto? Qual è la direzione dei due corpi dopo l'urto?
- Esercizio 6
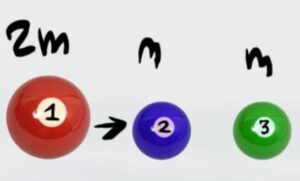
Tre palline di massa $m_1=2m, m_2=m, m_3=m$ si trovano su un piano. Le palline 2 e 3 sono inizialmente ferme quando vengono urtate dalla pallina 1 che viaggia alla velocità $v_1=10m/s$. La pallina 1 urta la pallina 2 che, a sua volta, urta la pallina 3.
Qual è la velocità finale della terza palla?
- Esercizi 7
Una macchina di massa $m_A=732kg$ inizialmente ferma, viene tamponata da un furgone di massa $m_F=1720kg$ che va ad una velocità $v_F=15,5m/s$. L'urto è completamente elastico.
Calcola la velocità del furgone e della macchina dopo l'urto.

- Esercizio 8
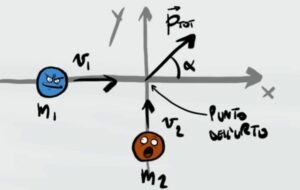
Due palline di massa nota $m_1$ e $m_2$ si muovono alla velocità $v_1$ e $v_2$. La pallina 1 si muove lungo l'asse x negativo mentre la pallina 2 lungo l'asse y negativo e si urtano nell'origine degli assi. Dopo l'urto anelastico (viene dispersa energia cinetica) le due palline si allontanano formando tra di loro un angolo incognito α.
Qual è la velocità finale del sistema formato dalle due palline? Qual è l'angolo α che si forma dopo l'urto?