TEORIA: Principio di Archimede
Il principio di Archimede afferma che un corpo immerso in un fluido riceve una spinta verso l'alto data dal peso del fluido spostato.
$F=d_FV_Cg$
In pratica quando noi immergiamo un corpo in un fluido stiamo occupando con il volume del corpo un volume che prima apparteneva al fluido, di conseguenza questo volume di fluido eserciterà sul corpo una forza per opporsi al peso.
Questa forza si oppone alla forza peso e tramite alcune semplificazioni otteniamo che il corpo galleggia solo le sua densità è minore o uguale alla densità del fluido. Per sapere quale porzione di volume del corpo è immersa nel liquido basta usare la seguente proporzione:
$\frac{V}{V_{IM}}=\frac{d_F}{d_C}$
Dove $d_F$ è la densità del fluido, $d_C$ la densità del corpo, $V$ il volume totale e $V_{IM}$ il volume immerso.
- Esercizio 1
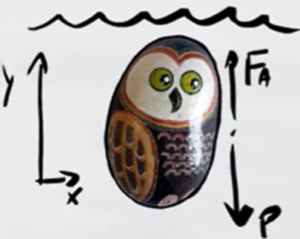
Se un corpo di massa $m=10kg$ e volume $V=0,002m^3$ viene immerso in acqua (densità $d=1000$ $kg/m^3$), galleggia oppure affonda?
- Esercizio 2 (dinamica)
La nasa lancia un pallone sonda riempito di elio di densità $d_C=0,18$ $kg/m^3$ in aria (densità dell'aria $d_F=1,22$ $kg/m^3$). Il pallone ha volume $V=600m^3$. Qual è l'intensità della forza totale che agisce sulla sonda?
- Esercizio 3 (dinamica)
Un corpo di massa $m=10kg$ e di volume $V=0,002m^3$ viene immerso in acqua. Calcola l'accelerazione del corpo in acqua
- Esercizio 4
Una biglia di piombo di densità $d_C=11,3$ $g/cm^3$ è immersa in un tubo contenente mercurio di densità $d_F=13,6$ $g/cm^3$. Calcola la percentuale di volume della biglia di piombo che è emersa
- Esercizio 5
Un blocco di legno di densità $d_C=1500$ $kg/m^3$, contenuto all'interno di un recipiente, è immerso per il 90% del suo volume in acqua (densità $d_{F_1}=1000$ $kg/m^3$). Qual è la frazione di legno immerso se si aggiunge uno strato di olio di densità $d_{F_2}=875$ $kg/m^3$ al recipiente?

- Esercizio 6
Una palla di cannone di ferro di densità $d_C=7800$ $kg/m^3$ ha una cavità al suo interno. Sapendo che la sua massa è $m=0,78kg$ e, immergendolo in mare, perde 1,56N di peso rispetto a prima, calcola il volume della cavità

- Esercizio 7
Una sfera di rame di densità $d_C=8900$ $kg/m^3$ galleggia sul mercurio di densità $d_F=13.600$ $kg/m^3$ e i 5/6 del suo volume emergono dal mercurio. Verifica se la sfera è piena o presenta una cavità

