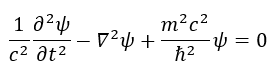Anche l’energia può essere quantizzata in dei pacchetti più semplici tramite l’equazione di Planck:
![]()
In cui h è la costante di minima azione, cioè l’energia minima che una particella emette percorrendo il tratto più veloce per andare da un punto A ad un punto B ed è all’incirca
![]()
Dividendo e moltiplicando ambo i membri per 2π otteniamo un’equazione che contiene anche l’operatore momento (cioè una trasformazione lineare che contiene la derivata nel tempo)
![]()
In meccanica quantistica le grandezze dinamiche sono rimpiazzate da trasformazioni lineari che vengono applicate sui vettori che rappresentano i movimenti lineari e rotatori della particella.
Nello spazio degli impulsi l’operatore x è rimpiazzato da:
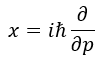
Mentre nello spazio delle x e del tempo l’impulso (la quantità di moto quantizzata) è rimpiazzato da:
![]()
L’operatore momento è il seguente:
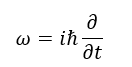
Per cui la formula dell’energia relativistica si può riscrivere usando le grandezze quantizzate
![]()
Quantizzando gli operatori E, P e portando tutto a destra per poi moltiplicare tutti i termini per
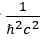
Otteniamo l’equazione di Klein-Gordon:
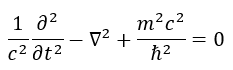
Per poter avere dei fini pratici questa equazione va legata con una funzione d’onda