- Esercizio 1
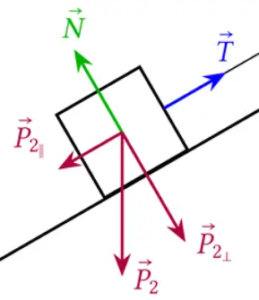
Per prima cosa dobbiamo considerare tutte le forze che agiscono sulla scatola: forza peso, reazione vincolare e forza di attrito. Siccome stiamo considerando un piano inclinato dobbiamo scomporre il peso nelle sue due componenti
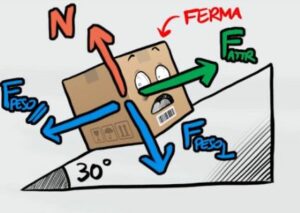
Dal grafico si può vedere che l'unica forza che si oppone all'attrito (colorato in verde) è la forza peso parallela.
$F_a=mgsin(30°)$
$F_a=15kg\cdot 9,81N/kg \cdot sin(30)°=74N$
- Esercizio 2
Per prima cosa disegniamo tutte le forze che agiscono sul corpo
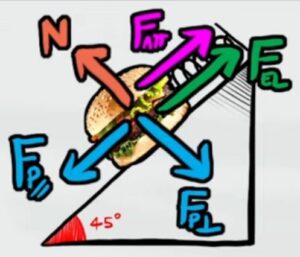
Dove Fp parallela è mgsin(45°) mentre Fp perpendicolare è mgcos(45°)
EQUILIBRI DELLE FORZE
Dalla foto possiamo scrivere l'equilibrio delle forze sapendo che sono uguali tutte le forze che sono opposte tra loro
EQUILIBRIO ASSE X →$mgsin(45°)=F_A+F_E$
EQUILIBRIO ASSE Y → $mgcos(45°)=N$
RICAVARE LA FORZA DI ATTRITO
Dove $F_A$ è la forza di attrito e $F_E$ è la forza elastica.
La forza di attrito la possiamo calcolare usando il coefficiente di attrito statico fornito dai dati
$F_A=μ_S\cdot N$
La reazione vincolare la ricaviamo dall'equilibrio sull'asse Y
$F_A=μ_S\cdot mgcos(45°)=2,77N$
RICAVARE LA FORZA ELASTICA
In questo modo possiamo ricavare la forza elastica tramite l'equilibrio sull'asse X
$mgsin(45°)=F_A+F_E$
Da questa equazione ricaviamo $F_E$
$F_E=mgsin(45°)-F_A=13,87N-2,77N$
$F_E=11,1N$
SOLUZIONE
Dalla formula della forza elastica
$F_E=kΔx$
Conosciamo la forza elastica e la costante elastica (ricavata dai dati del problema), quindi possiamo ricavare l'allungamento della molla
$Δx=\frac{F_E}{k}=0,28m$
- Esercizio 3
Per prima cosa disegniamo tutte le forze, considerando anche l'attrito
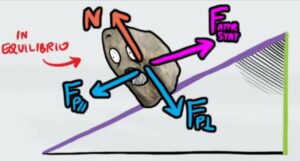
Scriviamo le equazioni che permettono l'equilibrio su entrambi gli assi (dove $F_a$ è la forza di attrito)
EQUILIBRIO ASSE Y → $N-P_y=0$
EQUILIBRIO ASSE X → $F_a+T-P_x=0$
Calcoliamo le due componenti del peso (ricordando che nel piano inclinato la componente Y si calcola con il coseno e la componente X con il seno)
$P_x=mgsin(10°)=8,52N$
$P_y=mgcos(10°)=48,3N$
RICAVARE L'ATTRITO
Dall'equilibrio sull'asse y possiamo ricavare la reazione vincolare.
$N=P_x=48,3N$
Ora che abbiamo la reazione vincolare possiamo ricavare la forza di attrito statico massima dalla formula
$F_a=μ_sN=4,84N$
RICAVARE LA TENSIONE
Ora abbiamo tutte le forze tranne la tensione che si può ricavare dall'equilibrio sull'asse X
$F_a+T-P_x=0$
$T=P_x-F_a=3,68N$
- Esercizio 4
Per prima cosa disegniamo le 4 forze principali in ognuno delle due casse; la reazione vincolare, le due componenti delle forze peso e la tensione del filo.
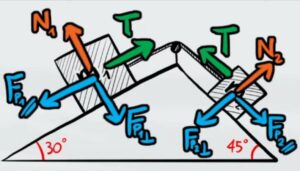
Adesso le due forze di attrito dei due corpi dipendono in base a come si evolve il problema. Infatti ci sono due casi: il primo in cui la cassa 1 vince sulla cassa 2 e scivola sul piano inclinato trascinando con se la cassa 2 o viceversa.

Per poterlo capire dobbiamo capire quale delle due forze prevale sull'altra. Dal grafico delle forze possiamo vedere che l'unica forza che tende a far scivolare le due casse dal piano è la componente X del peso.
Quindi per poter capire quale forza vince sull'altra basta calcolare le forze peso X e confrontare i risultati
MASSA 1 $P_x=m_1gsin(30°)=49N$
MASSA 2 $P_x=m_2gsin(45°)=42N$
Quindi la cassa 1 vince sulla cassa 2, quindi l'attrito deve bilanciare il peso della cassa 1
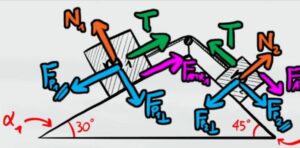
EQUILIBRIO
Ora possiamo scrivere le condizioni di equilibrio sui due assi. Dove $F_A$ sono le forze di attrito.
Le forze rivolte verso sinistra le mettiamo con segno positivo e quelle rivolte verso destra con segno negativo.
EQUILIBRIO ASSE X → $P_{1x}-F_{A1}-T+T-P_{2x}-F_{A2}=0$
$P_{1x}-F_{A1}-P{2x}-F_{A2}=0$
L'equilibrio sull'asse X descrive l'intero sistema di 2 casse mentre l'equilibrio sull'asse Y considera le singole casse in quanto il movimento sull'asse Y di una non influenza quello dell'altro. L'equilibrio sull'asse Y delle due casse risulta essere:
$P_{1y}-N_1=0$
$P_{2y}-N_2=0$
Dall'equilibrio sull'asse Y ricaviamo le due reazioni vincolari
$N_1=m_1gcos(30°)=85N$
$N_2=m_2gcos(45°)=41,6N$
Avendo le reazioni vincolari possiamo riscrivere le due forze di attrito minime come
$F_{A1}=N_1μ_s$
$F_{A2}=N_2μ_s$
Possiamo inserire queste due forze di attrito nell'equilibrio sull'asse X
$P{1x}-N_1μ_s-P{2x}-N_2μ_s=0$
Di questa equazione abbiamo tutte le incognite tranne il coefficiente di attrito statico, che possiamo ricavare risolvendo l'equazione. Per prima cosa raccogliamo il coefficiente
$-μ_s(N_1+N_2)+P{1x}-P{2x}=0$
$-μ_s(N_1+N_2)=-P{1x}+P{2x}=0$
$μ_s(N_1+N_2)=P{1x}-P{2x}=0$
Risolvendo otteniamo
$μ_s=\frac{P_{1x}-P_{2x}}{N_1+N_2}$
Sostituendo tutti i termini con quello che abbiamo ricavato otteniamo questa espressione:
$μ_S=\frac{m_1gsin(30°)-m_2gsin(45°)}{m_1gcos(30°)+m_2gcos(45°)}$
Sia al numeratore e al denominatore si può raccogliere g e semplificarla
$μ_S=\frac{m_1sin(30°)-m_2sin(45°)}{m_1cos(30°)+m_2cos(45°)}$
- Esercizio 5
Per avere l'equilibrio la forza di attrito statica deve essere uguale alla forza che si oppone, cioè la componente X del peso
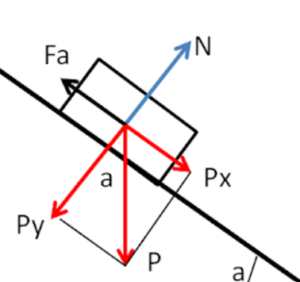
Adesso scriviamo le due equazioni per l'equilibrio delle forze sull'asse Y ($N$ e $P_y$) e le forze sull'asse X ($F_a$ e $P_x$).
EQUILIBRIO ASSE Y → $N=P_y$
EQUILIBRIO ASSE X → $F_a=P_x$
A questo punto possiamo porre che l'attrito statico è massimo quando raggiunge l'equilibrio, quindi possiamo usare la formula
$F_a=μ_SN$
La reazione vincolare la ricaviamo dall'equilibrio sull'asse Y
$N=P_y=mgcos(40°)$
Quindi
$F_a=μ_Smgcos(40°)$
Ora possiamo inserire questa espressione al posto della forza di attrito nell'equilibrio sull'asse X
$F_a=P_x$
Diventa (sostituendo $P_x$ con $mgsin(40°)$):
$μ_Smgcos(40°)=mgsin(40°)$
A questo punto possiamo notare che sia a destra e a sinistra dell'equazione è presente il termine $mg$ che può essere semplificato
$μ_Scos(40°)=sin(40°)$
Da cui ricaviamo il minimo coefficiente di attrito statico per l'equilibrio
$μ_S=\frac{sin(40°)}{cos(40°)}=0,84$
Nel problema ci chiede per quali valori del coefficiente il corpo scivola dal piano. Siccome noi abbiamo ricavato il valore minimo per mantenere il corpo in equilibrio, per avere che il corpo scivoli dal piano il coefficiente deve essere minore rispetto a questo numero ottenuto.
IL CORPO SCIVOLA → $μ_S<0,84$
- Esercizio 6
Per prima cosa disegniamo tutte le forze presenti oscurando l'attrito
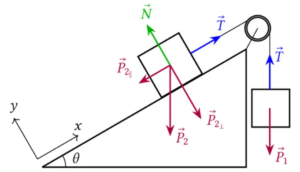
Per stabilire il verso della forza di attrito bisogna capire quale dei due pesi prevale sull'altro.
Nella massa 2 la forza che la fa scivolare dal piano è la componente X del peso (come si può vedere dal grafico). La massa 1, invece, non si trova su un piano inclinato, quindi non ha componenti della forza peso e l'unica forza che lo fa cadere verso il basso è $P_1$
$P_{2x}=m_2gsin(45°)=69,4N$
$P_1=m_1g=49N$
Tra le due forze prevale $P_{1x}$, quindi per mantenere l'equilibrio la forza di attrito deve essere opposta a $P_{1x}$.
Ora possiamo scrivere le equazioni che permettono l'equilibrio dei due corpi (NOTA: per risolvere questo problema basta utilizzare l'equilibrio X della massa 2)
MASSA 1 → $T+F_A-P_{2x}=0$
MASSA 2 → $T-P{1}=0$
Nell'equazione della massa 2 l'unica incognita è la tensione $T$ che possiamo facilmente ricavare
$T=P_1=m_1g$
Questo risultato lo possiamo mettere nell'equazione della massa 1 per trovare la forza di attrito
$m_1g+F_A-P{2x}=0$
Sviluppiamo l'espressione per $P_{2x}$
$m_1g+F_A-m_2gsin(45°)=0$
Da cui ricaviamo la forza di attrito
$F_A=m_2gsin(45°)-m_1g=20,32N$
- Esercizio 7
Per prima cosa disegniamo tutte le forze agenti sul sistema
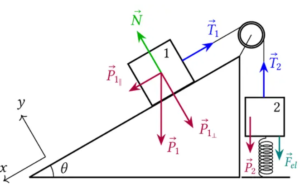
Per capire il verso della forza elastica bisogna stabilire quale delle due masse vince sull'altra.
Nel caso di m l'unica forza che tende a farlo cadere è la forza peso (P=mg) mentre nel caso di M l'unica forza che lo fa scivolare dal piano è la componente X del peso.
Queste sono le due forze peso da considerare:
$P_{1x}=m_1gsin(45°)=69,4N$
$P_2=m_2g=49N$
Dunque tra le due masse vince la massa 1 e siccome è più pesante tenderà a scivolare dal piano tirando verso l'alto la massa m tramite la fune con la quale sono collegate.
Quindi la molla verrà tirata verso l'alto dalla tensione della fune attaccata a m (guarda la figura) per cui la forza elastica, che è sempre opposta alla forza cha fa allungare la molla, sarà diretta verso il basso.
EQUILIBRIO
Per avere l'equilibrio tutte le forze delle due masse devono essere in equilibrio. Per avere l'equilibrio sulla massa 2 la tensione deve essere bilanciata dalla somma delle forze opposte
$T=F_{el}+P_2=F_{el}+mg$
Nel caso della massa 1 per avere l'equilibrio sull'asse X (l'equilibrio sull'asse Y non ci da informazioni importanti per poter risolvere il problema) la forza $P_{1x}$, che tende a farlo scivolare dal piano, deve essere bilanciata dalla forza opposta (la tensione).
$T=P_{1x}$
$T=m_1gsin(45°)=69,4N$
Ora che abbiamo la tensione possiamo ricavare la forza elastica dall'equilibrio della massa 2
$T=F_{el}+P_2$
Sostituiamo $P$ con $mg$ e ricaviamo la forza elastica
$F_{el}=T-m_2g=20,3N$
FORZA ELASTICA
L'esercizio però ci chiede l'allungamento totale della molla, quindi dobbiamo utilizzare la formula per la forza elastica
$F_{el}=kΔx$
Dove $Δx$ è la differenza tra l'allungamento totale della molla ($x$) e la lunghezza a riposo che ci viene fornita dai dati ($x_0$)
$Δx=x-x_0$
Quindi la forza elastica diventa
$F_{el}=k(x-x_0)$
Di questa equazione abbiamo tutti i dati tranne la lunghezza totale $x$ che si può ottenere risolvend0 questa equazione
$x-x_0=\frac{F_{el}}{k}$
$x=\frac{F_{el}}{k}+x_0=0,6m$
- Esercizio 8
Per prima cosa disegniamo tutte le forze agenti sul piano

Per il secondo principio della dinamica la somma di tutte le forze agenti su un corpo è uguale al prodotto di massa e accelerazione del corpo stesso.
$F_{TOT}=ma$
MASSA 1
Su $m_1$ le forze che agiscono sono la tensione ($T$) e il peso ($P_1$), quindi la loro somma è massa per accelerazione
$T-P_1=m_1a$
(Il meno va messo perché le due forze hanno verso opposto).
MASSA 2
La massa $m_2$ si trova su un piano inclinato, quindi ci sono due tipi di forze che agiscono su di essa: le forze sull'asse X e le forze sull'asse Y. Di questi due tipi di forze solo le forze sull'asse X generano un accelerazione perché è l'asse su cui la massa si muove
Siccome il corpo non si muove sull'asse Y, la somma di tutte le forze in Y è 0
ASSE X → $T-P_{2x}=m_2a$
ASSE Y → $N-P_{2y}=0$
SISTEMA DI EQUAZIONI
Le due incognite che dobbiamo trovare sono la tensione ($T$) e l'accelerazione dei due corpi ($a$). Entrambe queste forze sono uguali in tutte e due i corpi perché sono attaccati insieme da una fune, per cui si muovono insieme alla stessa accelerazione.
Le uniche due equazioni in cui sono presenti tensione e accelerazione sono l'equazione della massa 1 e l'equazione per l'asse X della massa 2, quindi possiamo metterle insieme nello stesso sistema di equazioni
$T-P_1=m_1a$
$T-P_{2x}=m_2a$
Sostituiamo i due pesi
$T-m_1g=m_1a$
$T-m_2gsin(45°)=m_2a$
Ora basta risolvere questo sistema di equazioni per trovare le due incognite. Dalla prima equazione
$T-m_1g=m_1a$
Ricaviamo la tensione
$T=m_1a+m_1g$
E la sostituiamo nella seconda equazione per ricavare l'accelerazione
$m_1a+m_1g-m_2gsin(45°)=m_2a$
Ora basta risolvere l'equazione per $a$
$m_1g-m_2gsin(45°)=m_2a-m_1a$
Giriamo l'equazione e raccogliamo $a$ a fattore comune
$a(m_2-m_1)=m_1g-m_2gsin(45°)$
Da qui ricaviamo $a$
$a=\frac{m_1g-m_2gsin(45°)}{m_2-m_1}=-4m/s^2$
Il segno meno indica semplicemente che l'accelerazione punta verso il basso (nel caso della massa 2 che scivola dal piano) e punta verso l'alto nel caso della massa 1 (che invece sta risalendo tramite la fune con cui sono attaccati)
Ora che abbiamo l'accelerazione la possiamo sostituire nell'equazione che abbiamo utilizzato prima per la tensione
$T=m_1a+m_1g$
Sostituendo le lettere con i valori numerici otteniamo (considerando il modulo dell'accelerazione)
$T=74,7N$
