PAGINA DI ESERCIZI: MOTO RETTILINEO UNIFORME
- Esercizio 1
PRIMA DOMANDA
Per trasformare la velocità da metri al secondo a chilometri orari basta moltiplicare per 3,6
$v=20m/s \cdot 3,6=72km/h$
SECONDA DOMANDA
Per sapere quanto spazio percorre in 15 minuti dobbiamo prima convertire il tempo in secondi, per farlo basta moltiplicare il tempo in minuti per 60
$Δt=15min \cdot 60=900s$
Adesso abbiamo la velocità in metri al secondo ($20m/s$) e il tempo in secondi. Quindi possiamo ricavare lo spostamento in metri dalla formula del moto
$v=\frac{Δx}{Δt}$
Da questa formula possiamo ricavare lo spostamento
$Δx=v\cdot Δt=18.000m=18km$
- Esercizio 2
Per prima cosa dobbiamo convertire i due tempi in secondi moltiplicando i minuti per 60
$Δt_1=3min \cdot 60 +20s=200s$
$Δt_2=4min \cdot 60 +10s=250s$
E adesso possiamo calcolare le due velocità conoscendo lo spostamento ($Δx_1=800m$ e Δx_2=1000m$) e il tempo impiegato
$v_1=\frac{Δx_1}{Δt_1}=4m/s$
$v_2=\frac{Δx_2}{Δt_2}=4m/s$
Le due velocità sono uguali, quindi i due atleti sono arrivati pari.
- Esercizio 3
Per poter calcolare la velocità media durante tutto il tragitto bisogna conoscere lo spostamento totale e il tempo totale impiegato
$v_M=\frac{Δx_{tot}}{Δt_{tot}}$
Lo spostamento totale lo otteniamo sommando i due spostamenti
$Δx_{tot}=200km+100km=300km$
Per calcolare i due tempi impiegati conoscendo la velocità e lo spostamento, dobbiamo usare la formula del moto
$v=\frac{Δx}{Δt}$
Da cui ricavare il tempo
$Δt=\frac{Δx}{v}$
In questo modo possiamo calcolare i due tempi impiegati
$Δt_1=\frac{Δx_1}{v_1}=6,7h$
$Δt_2=\frac{Δx_2}{v_2}=1,7h$
Facendo la somma dei due tempi impiegati possiamo ricavare il tempo totale
$Δt_{tot}=6,7h+1,7h=8,4h$
Ora che abbiamo ricavato il tempo totale impiegato e lo spostamento totale possiamo calcolare la velocità media
$v_M=\frac{Δx_{tot}}{Δt_{tot}}=35,7km/h$
- Esercizio 4
Siccome la velocità è in km/h ci conviene convertire i minuti in ore dividendo per 60
$10min ÷ 60=0,17h$
Dalla formula della velocità
$\vec{v}=\frac{Δ\vec{x}}{Δt}$
Possiamo ricavare gli spostamenti delle due macchine, sapendo che i due tempi sono uguali e corrispondono a 0,17h
$Δ\vec{x}_1=\vec{v}_1\cdot Δt=17km$
$Δ\vec{x}_2=\vec{v}_2\cdot Δt=20,4km$
Siccome gli spostamenti sono due vettori che formano un angolo di 90° tra loro, il vettore somma si calcola con il teorema di Pitagora
$Δx_{tot}=\sqrt{(Δx_1)^2+(Δx_2)^2}=26,55km$
- Esercizio 5
Se un uomo percorre 50 metri in 10 secondi, la sua velocità sarà data dal rapporto tra la distanza percorsa e il tempo impiegato
$v=\frac{d}{Δt}=5m/s$
Per calcolare quanto spazio percorre in 1 ora bisogna prima convertire un'ora in secondi
$1ora \cdot 60min \cdot 60s= 3600s$
Dala formula della velocità ricaviamo lo spazio percorso in un'ora
$d=v\cdot Δt=5m/s \cdot 3600s=18.000m$
Se vogliamo possiamo convertirlo in km
$d=18km$
- Esercizio 6
Dalla legge oraria del moto sappiamo che la posizione finale è data da
$x_f=x_i+vt$
Quello che ci chiede il problema è ricavare la funzione che descrive lo spostamento in funzione del tempo e per farlo dobbiamo ricavare la posizione inziale $x_i$ e la velocità $v$.
POSIZIONE INZIALE
La posizione inziale è il punto in cui il corpo si trova a $t=0s$. Dal grafico si può vedere che la posizione iniziale è 60 metri. Perché è questo il punto in cui inizia la retta
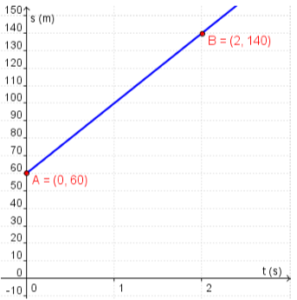
Quindi nell'equazione del moto possiamo già inserire la posizione iniziale
$x_f=60+vt$
VELOCITA'
Dalla formula del moto la velocità è data dal rapporto tra spazio percorso e tempo impiegato
$v=\frac{Δx}{Δt}$
Lo spazio percorso è la differenza tra posizione finale e inziale
$Δx=x_f-x_i$
E la stessa cosa vale per il tempo impiegato
$Δt=t_f-t_i$
Come si può vedere dal grafico il punto finale è B mentre il punto di inizio è A. Quindi la velocità è
$v=\frac{x_B-x_A}{t_B-t_A}$
Il punto B ha posizione $x_B=140m$ a $t=2s$ mentre A ha posizione $x_A=60m$ a $t=os$.
Sostituendo nella formula della velocità otteniamo
$v=\frac{140-60}{2-0}=40m/s$
LEGGE ORARIA
Sostituendo la velocità ricavata nella legge oraria del moto otteniamo
$x_f=60+40t$
In questo modo abbiamo ottenuto l'equazione della retta che descrive la posizione del corpo in funzione del tempo.
- Esercizio 7
In un grafico in cui si conoscono velocità e tempo, lo spazio percorso sarà dato dall'area sotto le curve
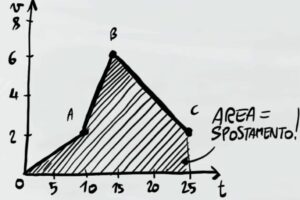
Per semplificare il problema possiamo dividere il grafico in tre figure geometriche nei punti A,B e C
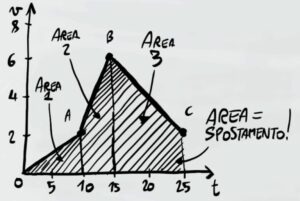
Per poter calcolare lo spostamento totale dobbiamo quindi calcolare le tre aree del grafico e sommarle.
La prima area è un triangolo quindi l'area è
$A_1=\frac{base\cdot altezza}{2}$
Dove la base è la differenza di tempo e l'altezza la differenza di velocità
$A_2=\frac{(10-0)(2-0}{2}=10m$
(NOTA: anche se si tratta di un'area l'unità di misura è metri e non metri quadri perché si semplificano le unità di misura di velocità e tempo)
La seconda e la terza area sono dei trapezi quindi le loro aree sono
$A=\frac{(base 1 + base 2)\cdot altezza}{2}$
Per semplicità basta guardare i due trapezi orizzontalmente in modo tale che le due basi siano le velocità e che le altezze siano i due tempi
Quindi per L'area 2 la formula diventa
$A_2=\frac{[(6-0)+(2-0)](15-10)}{2}=20m$
$A_3=\frac{[(2-0)+(6-0)](25-15)}{2}$
- Esercizio 8
Per prima cosa dobbiamo scegliere un punto di riferimento, che per comodità possiamo scegliere la casa da cui parte il padre.
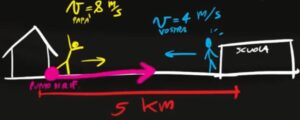
In questo modo tutte le velocità verso destra (quella del padre) sono positive mentre quelle verso sinistra (velocità del figlio) sono negative.
Ora che abbiamo scelto il sistema di riferimento possiamo scrivere le due leggi orarie del moto per le due persone
PADRE → $x_{p_f}=x_{p_i}+v_pΔt_p$
FIGLIO → $x_{F_f}=x_{F_i}+v_FΔt_F$
La posizione inziale è la distanza a cui si trova la persona all'inizio dal punto di riferimento. Quindi nel nostro caso il padre ha posizione inziale 0 perché parte dal punto di riferimento mentre il figlio parte da 5km di distanza
$x_{p_f}=v_pΔt_p$
$x_{F_f}=5000+v_FΔt_F$
$Δt$ indica la differenza tra il tempo che ci impiega a percorrere il tratto e il ritardo
$Δt=t_f-t_R$
Nel caso del figlio il tempi di ritardo è 0 mentre il padre inizia con 5 minuti di ritardo (300 secondi)
$x_{p_f}=v_p(t_f-300)$
$x_{F_f}=5000+v_Ft_f$
I due si incontrano allo stesso tempo, quindi i due tempi finali $t_f$ sono uguali. Inoltre si incontrano anche nello stesso punto, quindi la posizione finale dei due è uguale
$x_f=v_p(t_f-300)$
$x_f=5000+v_Ft_f$
Adesso possiamo sostituire le due velocità con quelle date dal problema
$x_f=8(t_f-300)$
$x_f=5000-4t_f$
(NOTA: il segno meno va messo perché la velocità del figlio è negativa)
Siccome le due posizioni finali sono uguali possiamo uguagliare le due espressioni e ricavare il tempo impiegato
$8(t_f-300)=5000-4t_f$
$8t_f-2400=5000-4t_f$
$12t_f=7400$
Quindi otteniamo che il tempo impiegato corrisponde a
$t_f=617s$
Sostituendo nella formula del moto del padre
$x_f=8(t_f-300)$
Otteniamo che i due si incontrano alla posizione
$x_f=2536m$
