PAGINA DI TEORIA: CINEMATICA
Il moto rettilineo uniformemente accelerato è un tipo di moto caratterizzato da spostamento, velocità e accelerazione.
L'accelerazione indica la variazione di velocità nel tempo e si misura in metri al secondo quadro ($m/s^2$). L'accelerazione è un vettore che ha stesso verso e direzione della velocità
$\vec{a}=\frac{Δv}{Δt}$
La variazione di velocità e di tempo si calcolano facendo la differenza tra istante finale e istante inziale
$\vec{a}=\frac{v_f-v_i}{t_f-t_i}$
Se l'accelerazione è positiva, la velocità sta aumentando mentre se è negativa la velocità sta diminuendo
Le leggi orarie del moto uniformemente accelerato sono tre:
POSIZIONE FINALE
$x_f=x_i+v_it+\frac{1}{2}at^2$
VELOCITA' FINALE
$v_f=v_i+at$
VARIAZIONE DI SPOSTAMENTO CONOSCENDO VELOCITA' E ACCELERAZIONE
$Δx=\frac{v_{f}^2-v_{i}^2}{2a}$
MOTO VERTICALE
Nel caso di un corpo sospeso in aria, la sua accelerazione sarà l'accelerazione di gravità $g$
L'accelerazione gravitazionale punta verso il basso, quindi stando ad un sistema di riferimento in cui i vettori verso l'alto sono positivi, l'accelerazione sarà negativa
$x_f=x_i+v_it-\frac{1}{2}gt^2$
$v_f=v_i-gt$
- Esercizio 1 (moto accelerato)
Un aereo ha un'accelerazione $a=2,2 m/s^2$ e una velocità di decollo $v_d=95 m/s$. Calcola la minima variazione di spostamento per decollare.

- Esercizio 2 (moto accelerato)
Una nave si muove di moto rettilineo con accelerazione costante, la nave parte da ferma e raggiunge la velocità finale $v_f=4,12 m/s$. Qual è la velocità media della nave?

- Esercizio 3 (moto accelerato)
La stessa nave dell'esercizio 2 ha raggiunto la sua velocità finale ($4,12 m/s$) partendo da ferma in $4,77$ secondi. Quanto spazio ha percorso?
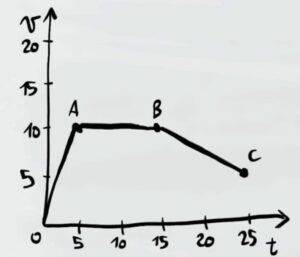
- Esercizio 4 (grafico)
Il seguente grafico rappresenta la variazione della velocità nel tempo di un corpo in vari punti del suo tragitto. Calcola l'accelerazione in ogni punto.
- Esercizio 5 (moto verticale)
Un vulcano lancia un lapillo verso l'alto ad una velocità inziale $v_i=28 m/s$. Calcola la velocità del lapillo dopo $t_1=2 s$ dal lancio e dopo $t_2=3 s$.

- Esercizio 6 (moto verticale)
Una pallina da tennis cade da un edificio alto $9,5 m$ e rimbalza sul suolo con una velocità $v=8,4 m/s$.
a) Calcola la velocità con cui la pallina arriva a terra
b) Calcola quanto tempo ci mette la pallina a cadere dall'edificio
c) Qual è l'altezza massima che raggiunge la pallina dopo il rimbalzo?
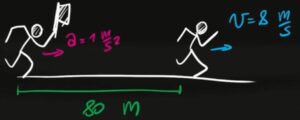
- Esercizio 7 (moto accelerato con due corpi)
Mario scappa dalla nonna dopo che ha detto di essere pieno e di non volere più nient'altro da mangiare. Mario parte da $80 m$ di distanza dalla nonna e va alla velocità costante $v=8 m/s$.
La nonna invece si muove di moto accelerato e, partendo da ferma, lo insegue con accelerazione $a= 1 m/s^2$
a) Dopo quanto tempo la nonna raggiunge Mario?
b) Quanta strada fa Mario prima di essere preso?
c) Con che velocità la nonna lo raggiunge?