Il problema equivale a trovare gli angoli per cui, se non ci fosse il muro, la gittata sarebbe la somma dello spazio inziale prima di colpire il muro (15 metri) e lo spazio che percorre dopo aver rimbalzato contro il muro stesso.
$G=15+75,44=90,44 m$
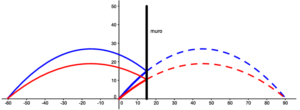
Dalla formula della gittata possiamo ricavare gli angoli di inclinazione della parabola
$G=\frac{2v_xv_y}{g}$
Per prima cosa sostituiamo le due componenti con le funzioni seno e coseno
$v_x=vcos(θ)$
$v_y=vsin(θ)$
In questo modo la gittata diventa
$G=\frac{2v^2cos(θ)sin(θ)}{g}$
Dalle formule di duplicazione abbiamo
$sin(θ)cos(θ)=\frac{1}{2}sin(2θ)$
Sostituendo nella formula della gittata otteniamo
$G=\frac{v^2sin(2θ)}{g}$
Da questa formula possiamo ricavare il seno dell'angolo
$Gg=v^2sin(2θ)$
$sin(2θ)=\frac{Gg}{v^2}$
Per trovare il valore di $2θ$ bisogna applicare la funzione inversa del seno
$2θ=arcsin(\frac{Gg}{v^2})$
$θ=\frac{1}{2}arcsin(\frac{Gg}{v^2})$
Sostituendo i valori numerici si ottengono due possibili angoli da cui è stato lanciato il pallone
$θ_1=40°$
$θ_2=50°$
