La pallina cade da un altezza di 1,4 m e con la sua traiettoria crea una parabola fino a toccare terra
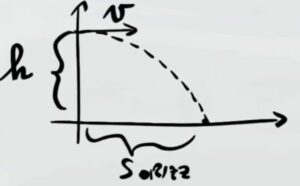
Lo spazio orizzontale percorso dalla pallina è $S_{orizz}=8,75 m$. Lo spazio orizzontale non dipende dalla gravità ed è quindi descritto dalla legge del moto rettilineo uniforme
$S_{orizz}=S_i+vt$
Come si può vedere dal grafico la pallina parte da $x=0$ quindi ha spostamento inziale nullo
$S_{orizz}=vt$
Da questo possiamo ricavare il tempo che ci mette la pallina a cadere
$t=\frac{S_{orizz}}{v}=1,26s$
L'altezza invece dipende dall'accelerazione gravitazionale e si muove di moto rettilineo accelerato
$h_f=h+v_it-\frac{1}{2}gt^2$
La pallina alla fine cade a terra, quindi l'altezza finale è 0
$0=h+v_it-\frac{1}{2}gt^2$
Nel problema non si hanno dati sulla velocità inziale, quindi possiamo presupporre che la pallina parte da ferma con velocità inziale 0 e inizia a muoversi per effetto della gravità
$0=h-\frac{1}{2}gt^2$
$h=\frac{1}{2}gt^2$
In questa equazione conosciamo il tempo e l'altezza da cui la pallina cade, quindi possiamo ricavare l'accelerazione gravitazionale del pianeta
$g=\frac{2h}{t^2}=1,77 m/s^2$
