Per poter comprendere meglio la richiesta disegniamo il velodromo visto in sezione (cioè immaginiamoci di tagliarlo a metà in modo da poterlo vedere di lato)
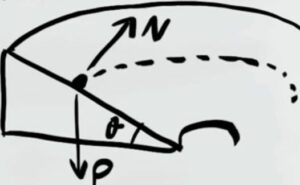
Si può vedere che il velodromo agisce come un piano inclinato di un angolo $θ$. Su questo piano la reazione vincolare si può dividere nelle sue due componenti
$N_x=Nsin(θ)$
$N_y=Ncos(θ)$
La componente Y è bilanciata dalla forza peso. La forza centripeta punta verso il centro del velodromo, quindi la componente X della reazione vincolare deve essere opposta al centro
$F_c=rmω^2$
La velocità angolare può essere sostituita con
$ω=\frac{v}{r}$
Ottenendo
$F_c=rm\frac{v^2}{r^2}=m\frac{v^2}{r}$
EQUILIBRIO DELLE FORZE
Ora che conosciamo le forze che agiscono sull'asse X ($N_x$ e $F_c$) e le forze che agiscono sull'asse Y ($P$ e $N_y$) possiamo scrivere le condizioni di equilibrio
$ASSE X→N_x=F_c$
$ASSE Y→N_y=P$
Sostituiamo ogni forza con la corrispettiva formula
$Nsin(θ)=m\frac{v^2}{r}$
$Ncos(θ)=mg$
Dalla seconda equazione possiamo ricavare la reazione vincolare
$N=\frac{mg}{cos(θ)}$
Per ricavare l'angolo θ, invece, dobbiamo fare il rapporto tra le due equazioni
$\frac{Nsin(θ)}{Ncos(θ)}=\frac{m\frac{v^2}{r}}{mg}$
Il rapporto tra seno e coseno è la tangente dell'angolo
$tan(θ)=\frac{v^2}{gr}$
Dunque l'angolo θ sarà uguale alla tangente inversa di questa grandezza che abbiamo ricavato
SIGNIFICATO FISICO
Le due formule che abbiamo ricavato sono
$tan(θ)=\frac{v^2}{gr}$
$N=\frac{mg}{cos(θ)}$
Per ricavare queste due formule abbiamo scritto che le componenti della reazione vincolare devono bilanciare il peso del corpo e la forza centripeta.
La reazione vincolare corrisponde alla resistenza del suolo. Quindi a livello fisico questo significa che il suolo del velodromo non deve solo reagire alla forza peso, ma deve anche fornire la forza centripeta necessaria affinché il moto rimanga circolare.
