Il moto circolare corrisponde al moto rettilineo uniforme e uniformemente accelerato per i corpi che ruotano.
VELOCITA' ROTAZIONALE
$ω=\frac{Δφ}{T}$
Dove T è il periodo di rotazione, cioè il tempo impiegato da un corpo per fare una rotazione completa e Δφ è lo spostamento angolare, cioè l'angolo in radianti percorso dal corpo.
ACCELERAZIONE ROTAZIONALE
$α=\frac{Δω}{Δt}$
Dove $Δt$ è il tempo impiegato per far variare la velocità angolare.
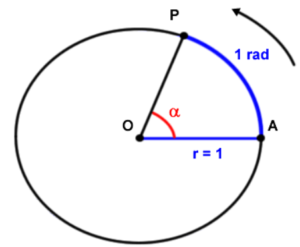
Le formule che legano la velocità e l'accelerazione angolare con quelle tangenziali (cioè $v$ e $a$ normali del moto rettilineo) sono le seguenti:
$a=αr$
$v=ωr$
Dove $r$ è il raggio della circonferenza su cui il corpo si muove
LEGGI ORARIE DEL MOTO (sono le varianti del moto rettilineo accelerato)
- Spostamento angolare finale
$φ_f=φ_i+ω_it+\frac{1}{2}αt^2$
- Velocità angolare finale (2 formule)
$ω=ω_i+αt$
$ω^2=ω_{i}^2+2αΔφ$
La forza che spinge un corpo in rotazione verso il centro è detta forza centripeta. La forza che bilancia la forza centripeta invece è la forza centrifuga, che spinge il corpo fuori dal centro.
$F_{centripeta}=rmω^2$
$F_{centrifuga}=-F_{centripeta}$
- Esercizio 1
Per pulire un'otturazione di un dente un dentista applica al trapano un disco abrasivo ruotante con un raggio $r=3,20 mm$ e con velocità angolare $ω=21500 rad/s$. Qual è la velocità tangenziale del bordo del disco? E a quanto corrisponde il periodo di rotazione del disco se la velocità del bordo vale $v_{b}=275 m/s$?
- Esercizio 2
Un lanciatore del disco parte da fermo ed inizia a ruotare con accelerazione angolare $α=2,2 rad/s$. Quanti giri sono necessari per raggiungere la velocità angolare di $ω=6,3 rad/s$? Quanto tempo ci impiega?

- Esercizio 3
Un disco di diametro $d=12 cm$ ruota su sé stesso ad una velocità angolare $ω=5,05 rad/s$. Quanto vale la velocità tangenziale del disco? Quanto vale l'accelerazione centripeta del disco?

- Esercizio 4
Un disco di diametro $d=12 cm$ accelera da 0 a una frequenza di 4 giri/s in 3 secondi. Qual è l'accelerazione del bordo del disco?
- Esercizio 5
Nell'atomo di idrogeno, l'elettrone orbita attorno al protone in una circonferenza di raggio $5,29\cdot 10^{-11} m$ con una velocità tangenziale $v=2,18\cdot 10^6 m/s$.
a) Qual è la velocità angolare dell'elettrone?
b) Quanti giri fa l'elettrone in 1 secondo?
c) Quanto vale l'accelerazione centripeta dell'elettrone?
- Esercizio 6
Le provette di una centrifuga che ruota con frequenza di 1000 giri al secondo contengono ognuno di loro un liquido su cui è sospesa una molecola di massa $m=10^{-22} kg$. Se le provette distano $0,1 m$ dal centro di rotazione, quanto vale la forza centrifuga esercitata su una singola molecola?

- Esercizio 7
Un punto materiale si muove lungo una circonferenza di raggio $r=1,8 m$ con un'accelerazione angolare $α_1=2,39 rad/s^2$. Dopo mezzo giro il corpo decelera fino a fermarsi completamente dopo aver percorso un altro mezzo giro.
a) Qual è l'accelerazione che assume il corpo durante il secondo mezzo giro quando inizia a decelerare?
b) Quanto tempo ci impiega a fare un giro completo?
c) Se nello stesso intervallo di tempo il moto fosse uniforme con accelerazione nulla, quale sarebbe l'accelerazione centripeta del punto?
- Esercizio 8
Trova la condizione che deve essere soddisfatta affinché un punto materiale lanciato con velocità $v$ su una pista inclinata come quella presente in un velodromo riesca a percorrere un arco di circonferenza con centro O.

