Il corpo attaccato alla molla esercita una forza continua che causa un allungamento e una compressione della molla. Questo movimento è definito dal moto armonico.
La molla parte da ferma, accelera fino a raggiungere la massima estensione, accelera nuovamente fino a raggiungere la posizione di riposo e poi decelera fino a fermarsi quando raggiunge la massima compressione
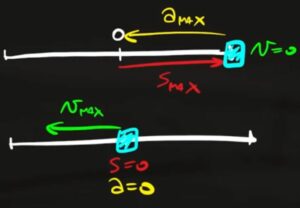
Quindi lo spostamento e l'accelerazione sono massimi nei due estremi mentre la velocità è massima al centro (cioè nella posizione di riposo della molla)
Per calcolare i valori massimi di queste tre variabili scriviamo le tre leggi orarie
$x_{max}=Rcos(ωt)$
$v_{max}=-Rωsin(ωt)$
$a_{max}=-Rω^2cos(ωt)$
Le funzioni seno e coseno possono variare solamente da -1 a 1. Quindi lo spostamento è massimo quando il coseno vale 1 mentre la velocità e l'accelerazione sono massime quando seno e coseno valgono -1 (in questo modo il meno si cancella con quello davanti e diventa positivo).
$x_{max}=R$
$v_{max}=Rω$
$a_{max}=Rω^2$
In pratica per poter ricavare i valori massimi delle tre variabili dobbiamo togliere le funzioni seno e coseno
Per poter calcolare i valori dobbiamo ricavare l'allungamento della molla (cioè R) e la pulsazione ω. la pulsazione la ricaviamo dalla formula
$ω=\sqrt{\frac{k}{m}}=44,7 rad/s$
Per l'allungamento invece dobbiamo utilizzare la formula della forza elastica e rimpiazzare lo spostamento con R
$F=kx$
$F=kR$
La forza che funge da forza elastica è data nel problema ed è $F=80 N$, quindi da questa formula possiamo ricavare R
$R=\frac{F}{k}=0,8 m$
Sostituendo questi due valori che abbiamo ricavato nelle tre leggi orarie ricaviamo
$x_{max}=0,8 m$
$v_{max}=35,8 m/s$
$a_{max}=1598,5 m/s^2$
