Il momento di inerzia è una grandezza fisica che indica la resistenza di un corpo rigido alla variazione del suo stato di rotazione rispetto a un asse. In altre parole, il momento di inerzia indica quanto difficile sia mettere in rotazione un oggetto o fermare la rotazione una volta che ha iniziato girare e si misura in chilo al metro quadro $kg\cdot m^2$.
Il momento di inerzia ha formula differente in base all'oggetto che si sta considerando.
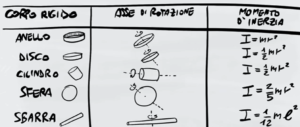
Se un oggetto non ha nessuna di queste forme si può usare la formula più generale:
$I=mr^2$
Dove $M$ è la massa dell'oggetto e $R$ il suo raggio. In generale la formula del momento di inerzia si può calcolare come l'integrale del prodotto tra il quadrato del raggio e l'infinitesimo della massa del corpo
$I=\int_Vr^2dm$
Il momento di inerzia è il corrispettivo della massa in dinamica, la somma di tutti i momenti applicati su un corpo è uguale al prodotto tra momento di inerzia e accelerazione angolare del corpo
$M_{tot}=Iα$
Le formule mostrate prima del momento di inerzia valgono per i corpi che ruotano intorno a se stessi. Il teorema di Huygens-Steiner permette di calcolare il momento di inerzia di un corpo che ruota attorno ad un asse che non è il suo centro
$I=I_{CM}+md^2$
Dove $I_{CM}$ è il momento di inerzia del centro di massa, $m$ è la massa del corpo che ruota e $d$ è la distanza tra il centro di massa e l'asse di rotazione
- Esercizio 1
Un disco di massa $m=50kg$ e raggio $r=1,8m$ ruota su sé stesso. Calcola il momento di inerzia del disco
- Esercizio 2
Calcola il momento di inerzia di una sfera di bronzo di raggio $r=5,7cm$ e densità $d=8,9\cdot 10^3$ $kg/m^3$ che ruota intorno al proprio centro.

- Esercizio 3
Il volano di una macchina a vapore ha massa $m=150kg$ e momento di inerzia $I=400$ $kg\cdot m^2$. Il volano ruota con velocità $v=30$ $m/s$ e ci mette 5 minuti per fermarsi. Qual è il momento dovuto all'attrito sull'asse del volano?

- Esercizio 4 (centro di massa)
Un disco di massa $m$ e di raggio $r$ scende srotolando un filo che non slitta rispetto al bordo del disco. Determina l'accelerazione del centro di massa e la tensione del filo
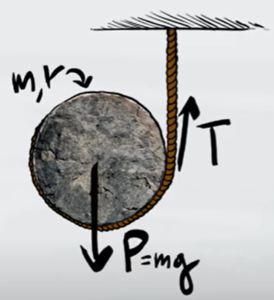
- Esercizio 5 (dinamica rotazionale)
Un disco sale lungo un piano inclinato di 45° con velocità inziale $v=5$ $m/s$. IL disco ha massa $m=1kg$ e raggio $r=0,5m$. Quanto tempo impiega a raggiungere il punto massimo sul piano inclinato prima di cadere giù per effetto della gravità?

- Esercizio 6 (dinamica rotazionale)
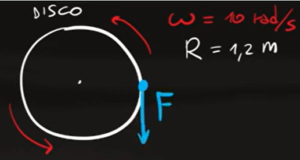
Su un disco di massa $m=20kg$ e raggio $r=1,2m$ ruota in senso antiorario con velocità angolare $ω=10$ $rad/s$. Per fermare il disco viene applicata una forza esterna che agisce in maniera tangenziale al disco di intensità $F=50N$ e che lo fa ruotare in senso orario.
a) Qual è la velocità angolare del disco?
b) Dopo quanto tempo il disco si ferma?
c) Quanti giri intorno al proprio asse fa il disco prima di fermarsi?
- Esercizio 7 (Huygens-Steiner)
Calcola il momento di inerzia di un sistema formato da due sfere uguali di massa $m$ e raggio $r$ collegate tra loro da una sbarra di lunghezza $l$ e massa $M$ e con asse di rotazione passante per il centro della sbarra

