Per poter calcolare il momento angolare del pendolo dobbiamo conoscere il momento di inerzia e la velocità angolare. Per il pendolo non c'è una formula specifica per il momento di inerzia, quindi possiamo utilizzare quella generale
$I=mr^2$
Dove il raggio in questo caso rappresenta la lunghezza del pendolo stesso, cioè $l=20cm$. Quindi il momento di inerzia del pendolo è:
$I=ml^2$
La velocità angolare invece la dobbiamo ricavare sfruttando la velocità orizzontale dai dati
RICAVARE LA VELOCITA' ANGOLARE
Per prima cosa possiamo calcolare l'angolo che si crea tra la velocità vettoriale del pendolo e la sua componente x (cioè la velocità orizzontale)
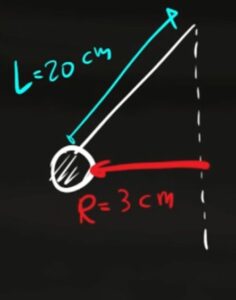
Come si può vedere nella figura tra il raggio R e la lunghezza L si forma un triangolo rettangolo dove la lunghezza del pendolo è l'ipotenusa e il raggio la base.
Usando la trigonometria sappiamo che la base è uguale al prodotto tra ipotenusa e il coseno dell'angolo θ
$R=lcos(θ)$
Da qui possiamo ricavare il coseno dell'angolo
$cos(θ)=\frac{R}{l}=0,15$
Applicando l'inverso del coseno calcoliamo il valore dell'angolo θ
$θ=arccos(\frac{R}{l})=81,37°$
Questo è l'angolo che si crea tra il pendolo il raggio e la lunghezza, possiamo ricavare l'angolo tra la velocità orizzontale e quella vettoriale sapendo che l'angolo tra la velocità vettoriale e il pendolo è 90° e che la somma di tutti gli angoli forma un angolo piatto di 180°.
Quindi l'angolo tra la velocità e la velocità orizzontale (chiamiamolo α) è la differenza tra l'angolo totale e i singoli angoli ricavati incluso l'angolo θ
$α=180°-90°-81,37°=8,63°$
Dalla formula della componente X della velocità:
$v_x=vcos(α)$
Possiamo calcolare la velocità vettoriale conoscendo la componente X e l'angolo α
$v=\frac{v_x}{cos(α)}=2,02$ $m/s$
Ora che abbiamo ricavato la velocità vettoriale possiamo calcolare la velocità angolare facendo il rapporto tra velocità e raggio di oscillazione
$ω=\frac{v}{r}$
Dove il raggio di oscillazione è la distanza tra il punto massimo di oscillazione e il punto di riposo, cioè $R$
$ω=\frac{v}{R}=67,3$ $rad/s$
RICAVARE IL MOMENTO ANGOLARE
Ora che abbiamo il momento di inerzia e la velocità angolare del pendolo possiamo ricavare il momento angolare
$L=Iω=ml^2ω=2,4\cdot 10^{-3}\frac{kg\cdot m^2}{s}$
