Il momento angolare è il corrispettivo della quantità di moto per le rotazioni e si calcola come il prodotto tra inerzia e velocità angolare
$L=Iω$
Infatti il momento di inerzia e la velocità angolare corrispondono alla massa e alla velocità in dinamica, per cui la formula corrisponde al prodotto tra massa e velocità, cioè la quantità di moto.
In assenza di momenti esterni come l'attrito, il momento angolare totale si conserva
$ΔL=0$
Quindi il momento angolare totale finale è uguale al momento angolare totale inziale
$L_{tot_f}=L_{tot_i}$
Nel caso in cui ci siano momenti esterni la quantità di moto totale è data dal prodotto tra momento e la variazione di tempo che si sta considerando
$ΔL=M_{tot}Δt$
- Esercizio 1
Un disco di massa $m=12g$ e raggio $r=6cm$ ruota con velocità lineare $v=10$ $m/s$. Calcola il suo momento angolare

- Esercizio 2
Su una sfera di raggio $r=2m$ viene applicata una forza tangenziale di intensità $F=30N$ che la fa ruotare attorno al proprio asse. Quanto vale il momento angolare della sfera dopo 5 secondi?

- Esercizio 3
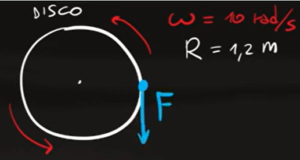
Un disco di raggio $R=1,2m$ e massa $m=2kg$ ruota attorno al proprio asse con velocità angolare inziale $ω_i=10$ $rad/s$ e per fermarlo viene applicata una forza tangenziale di intensità $F=10N$.
a) Dopo quanto tempo il disco si ferma?
b) Quanto momento angolare perde il disco dall'inizio della rotazione fino al momento in cui si ferma?
- Esercizio 4
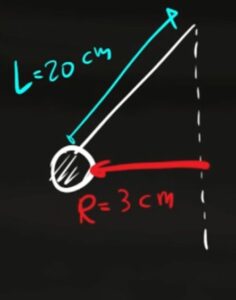
Un pendolo di massa $m=2kg$ oscilla attaccato ad un filo di lunghezza $l=20cm$. Quando il filo è distante 3 centimetri dal punto di riposo la velocità orizzontale del pendolo è $v_{orizz}=2$ $m/s$. Calcola il momento angolare del pendolo
- Esercizio 5
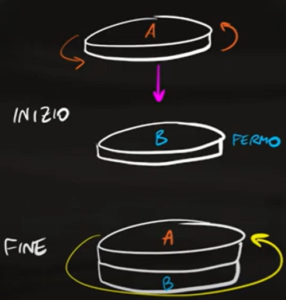
Un disco A di massa $m_a=0,8kg$ e raggio $r=0,5m$ sta ruotando con velocità angolare inziale $ω_{A_i}=40$ $rad/s$ sta sopra un disco B inizialmente fermo. Il disco B ha lo stesso raggio di A e massa $m_B=1,2kg$.
Ad un certo punto i disco A entra in contatto con il disco B e cominciano a ruotare insieme. Qual è la velocità angolare dei due dischi che ruotano uniti?
- Esercizio 6
Una giostra di massa $m=20kg$ e raggio $r=1,6m$ ruota attorno a se stessa con velocità angolare inziale $ω_i=15$ $rad/s$. Ad un certo punto una persona di massa $m=70kg$ sale sulla giostra e rimane ferma. Con che velocità angolare ruota la giostra dopo che la persona ci sale sopra?

