L’equazione dell’iperbole è la seguente:
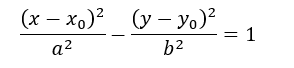
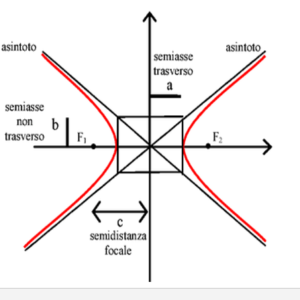
Gli asintoti sono delle rette che non intersecano mai l’iperbole ma si intersecano tra di loro nell’origine degli assi in modo tale da creare un rettangolo che ha come base la distanza tra le due parti dell’iperbole e come altezza la line che si crea collegando la parte destra e la parte sinistra dell’iperbole con gli asintoti come vien mostrato nella figura successiva (questa definizione vale per tutti i tipi di iperbole tranne quella equilatera).
La a rappresenta metà della base del rettangolo mentre la b rappresenta metà dell’altezza del rettangolo e c (anche se non compare nell’equazione) rappresenta metà della distanza tra i due fuochi.
Ci sono tra tipi di iperbole nel piano cartesiano:
1) Il primo tipo di iperbole è un luogo geometrico tale che
![]()
In questa iperbole la a > b e le coordinate dei fuochi sono le seguenti:
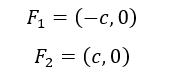
L’eccentricità indica quanto l’iperbole sia più schiacciata verso l'asse x e la formula è la seguente:
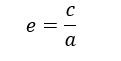
2) Il secondo tipo di iperbole è un luogo geometrico tale che
![]()
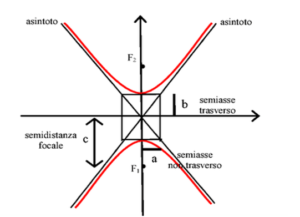
In questo tipo di iperbole b > a e le coordinate dei fuochi sono le seguenti:
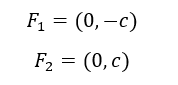
L’eccentricità indica quanto questo tipo di iperbole sia più schiacciato vero l’asse y e la formula è la seguente:
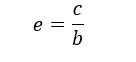
Inoltre sia nel primo che nel secondo tipo di iperbole l’equazione degli asintoti è la stessa :
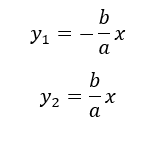
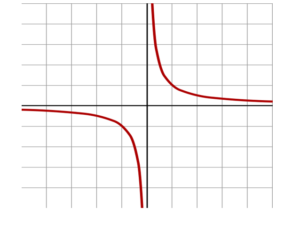
3) L’ultimo tipo di iperbole è l’iperbole equilatera che è differente dalle altre iperbole per l’equazione ma è simile perché si ricava ruotando uno dei due tipi di iperbole mostrate precedentemente.
Equazione dell’iperbole equilatera:
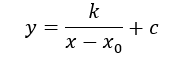
Più grande è c e più il centro dell’iperbole sarà alto nell’asse y mentre più k è grande e più l’iperbole sarà allargata mentre indica il centro dell’iperbole.
L’equazione degli asintoti sono:
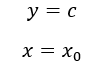
(nota: il secondo asintoto è una funzione parametrica con y = 0 e x = ).
Come si può vedere dall’immagine riportata qui sotto gli asintoti sono due rette costanti.