La distanza dell'immagine dalla lente e la distanza focali sono positive, quindi l'immagine e il fuoco si trovano davanti la lente rispetto a chi guarda
PRIMA DOMANDA
Conoscendo la distanza focale $f$ e la distanza dell'immagine dalla lente $d_0$ possiamo ricavare la distanza dell'oggetto reale dalla lente $d_0$ tramite la prima equazione delle lenti
$\frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}$
Isoliamo $d_0$ da questa equazione
$\frac{1}{d_0}=\frac{1}{f}-\frac{1}{d_i}$
Elevando entrambi i membri dell'equazione alla $(-1)$ otteniamo:
$d_0=(\frac{1}{f}-\frac{1}{d_i})^{-1}=-2,86$ $cm$
La distanza è negativa, quindi l'oggetto si trova dietro alla lente rispetto a chi guarda. Ora che abbiamo $d_0$ possiamo ricavare il fattore di ingrandimento facendo il rapporto tra $d_i$ e $d_0$
$G=-\frac{d_i}{d_0}=0,715$
SECONDA DOMANDA
La distanza dell'oggetto reale dalla lente l'abbiamo calcolata per rispondere alla prima domanda
$d_0=-2,86$ $cm$
TERZA DOMANDA
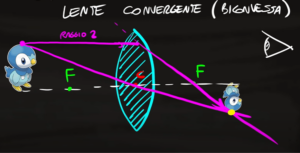
La lente è convergente, quindi l'immagine generata risulterà più piccola dell'oggetto reale ($G<1$) e si trova dal lato opposto rispetto all'oggetto. Questo l'abbiamo dimostrato sia tramite le equazione che tramite il disegno dei raggi all'inizio della pagina.
Dal disegno possiamo notare che il punto di incontro dei raggi si trova al di sotto dell'asse dei fuochi, quindi l'immagine generata risulterà capovolta.

