PRIMA DOMANDA
Dai dati ci viene data la lunghezza del raggio di curvatura dello specchietto, se approssimiamo lo specchietto ad una lente sferica possiamo ricavare la distanza focale della lente dividendo il raggio per 2
$f=\frac{r}{2}=-20$ $cm$
La distanza focale risulta negativa perché lo specchietto è convesso, quindi il fuoco si trova dietro lo specchietto. Ora che abbiamo la distanza focale possiamo ricavare la distanza tra l'immagine prodotta e la lente tramite la seconda equazione delle lenti
$\frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}$
Dove $d_0$ è la distanza tra la persona e la lente. Isolando $d_i$ dall'equazione otteniamo:
$\frac{1}{d_i}=\frac{1}{f}-\frac{1}{d_0}$
Per ricavare $d_i$ basta elevare alla $(-1)$ entrambi i lati dell'equazione
$d_i=(\frac{1}{f}-\frac{1}{d_0})^{-1}=-19,6$ $cm$
$d_i=-0,196m$
Anche la distanza dell'immagine è negativa, quindi anch'essa come il fuoco si trova dietro lo specchietto
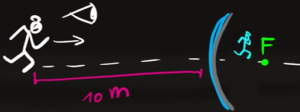
Facendo il rapporto tra la distanza dell'immagine dalla lente e la distanza della persona dalla lente otteniamo il fattore di ingrandimento $G$ con cui andremo a calcolare l'altezza dell'immagine $h_i$
$G=-\frac{d_i}{d_0}=0,0196$
Ora possiamo utilizzare la seconda equazione delle lenti per ricavare $h_i$
$G=\frac{h_i}{h_0}$
Risolvendo l'equazione otteniamo:
$h_i=Gh_0=0,39m$
Quindi l'altezza dell'immagine prodotta dalla lente è $h_i=39$ $cm$
SECONDA DOMANDA
La distanza dell'immagine dallo specchio è risultata negativa dai nostri calcoli, quindi l'immagine prodotta si trova dietro la lente convessa
