Per poter risolvere questo problema legato all'energia dobbiamo per prima cosa scrivere la conservazione del lavoro
$ΔE+ΔU=0$
Dove in questo caso l'energia potenziale è la somma di energia potenziale gravitazionale (data dal peso del blocco) ed energia elastica (data dalla molla)
$ΔU=U_{peso}+U_{molla}$
$ΔU=mgh_f-mgh_i+\frac{1}{2}kx_{f}^2-\frac{1}{2}kx_{i}^2$
Il blocco parte dal punto più basso, quindi $h_i=0$. Anche l'allungamento finale della molla vale 0 perché dopo aver rilasciato il blocco ritorna nella posizione di risposo senza alcun allungamento o compressione ($x_i=0$)
$ΔU=mgh_f-\frac{1}{2}kx_{i}^2$
L'energia cinetica invece ha sempre la stessa formula indipendentemente dal problema
$ΔE=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2$
Dove la velocità inziale è uguale a 0 perché il blocco parte da fermo e viene spinto dalla molla
$ΔE=\frac{1}{2}mv_{f}^2$
Quindi la conservazione del lavoro totale diventa
$\frac{1}{2}mv_{f}^2+mgh_f-\frac{1}{2}kx_{i}^2=0$
Adesso dobbiamo dividere il problema nei due casi possibili. Nel primo caso il blocco riesce non supera il piano inclinato e si ferma ad una certa altezza $h_f$ mentre nel secondo caso il blocco riesce a superare il piano e continua con una velocità finale incognita $v_f$. Proviamo a fare i calcoli nel primo caso per vedere se riesce a superare il piano
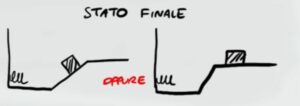
PRIMO CASO
Consideriamo il caso in cui il blocco si ferma ad una certa altezza del piano senza riuscire a superarlo. Se facendo i calcoli otterremo un altezza finale superiore rispetto all'altezza del piano vuol dire che il blocco riesce a superarlo e dovremmo rifare i calcoli per ricavare la velocità finale.
Dalla conservazione del lavoro:
$\frac{1}{2}mv_{f}^2+mgh_f-\frac{1}{2}kx_{i}^2=0$
Nel primo caso il blocco si ferma ad una certa altezza finale $h_f$, quindi la velocità finale è 0 ($v_f=0$)
$mgh_f-\frac{1}{2}kx_{i}^2=0$
Da questa equazione ricaviamo l'altezza finale
$mgh_f=\frac{1}{2}kx_{i}^2$
$h_f=\frac{kx_{i}^2}{2mg}=1,27 m$
Del piano inclinato conosciamo solamente la lunghezza, quindi dobbiamo ricavare l'altezza del piano utilizzando la trigonometria
$h_{piano}=lsin(45°)=1,13m$
Siccome l'altezza raggiunta dal blocco è superiore rispetto all'altezza del piano possiamo concludere che il blocco riesce a superare il piano e continua con velocità $v_f$.
RICAVARE LA VELOCITA' FINALE
Per poter ricavare la velocità finale dobbiamo riutilizzare la conservazione del lavoro utilizzata precedentemente
$\frac{1}{2}mv_{f}^2+mgh_f-\frac{1}{2}kx_{i}^2=0$
Dove questa volta l'altezza finale è l'altezza del piano (anche se il corpo riesce a superare questa altezza non vuol dire che va più in alto del piano stesso, una volta superato il piano il blocco procede verso destra come nell'immagine mostrata prima).
$\frac{1}{2}mv_{f}^2+mgh_{piano}-\frac{1}{2}kx_{i}^2=0$
Da questa equazione ricaviamo la velocità finale del blocco
$\frac{1}{2}mv_{f}^2=-mgh_{piano}+\frac{1}{2}kx_{i}^2$
$v_{f}^2=\frac{2}{m}(-mgh_{piano}+\frac{1}{2}kx_{i}^2)$
Applicando la radice quadrata ricaviamo la velocità finale
$v_f=\sqrt{\frac{2}{m}(-mgh_{piano}+\frac{1}{2}kx_{i}^2)}=1,67$ $m/s$
