PRIMA DOMANDA
Per calcolare il lavoro totale basta sommare l'energia cinetica totale e l'energia potenziale totale del blocco.
$L=ΔE+ΔU$
L'energia cinetica totale è la differenza tra energia finale ed iniziale
$ΔE=E_f-E_i$
$ΔE=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2$
Il blocco parte da fermo, per cui $v_i=0$. La velocità finale del blocco $v_f$ è la velocità nel punto A
$ΔE=\frac{1}{2}mv_{f}^2$
L'energia potenziale invece è composta da energia potenziale elastica (scambio di energia con la molla) ed energia potenziale gravitazionale (data dal peso del blocco)
$ΔU=U_{molla}+U_{peso}$
$ΔU=\frac{1}{2}kx_{f}^2-\frac{1}{2}kx_{i}^2+mgh_f-mgh_i$
Il blocco parte da fermo, per cui l'altezza iniziale è 0 ($h_i=0$) mentre l'altezza finale è l'altezza raggiunta nel punto A, cioè il raggio R come mostrato nella figura
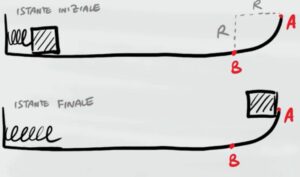
$h_f=R$
La molla parte compressa di 0,25 metri ma dopo aver rilasciato il blocco torna nella posizione di riposo per cui la compressione finale è nulla $x_f=0$. Quindi l'energia potenziale gravitazionale inziale e l'energia elastica finale sono uguali a 0, sostituendo nella formula dell'energia potenziale otteniamo
$ΔU=-\frac{1}{2}kx_{i}^2+mgR$
Sostituendo l'energia potenziale ricavata e l'energia cinetica nella formula del lavoro otteniamo
$L=\frac{1}{2}mv_{f}^2-\frac{1}{2}kx_{i}^2+mgR$
Sostituendo con i dati otteniamo
$L=-0,65J$
Il meno indica una perdita di energia del corpo per effetto dell'attrito.
SECONDA DOMANDA
L'accelerazione centripeta si può calcolare dalla formula
$a_c=\frac{v^2}{R}$
Dove la velocità in questione è la velocità nel punto A come richiesto dal problema. Sostituendo con i dati otteniamo
$a_c=14$ $m/s^2$
TERZA DOMANDA
Conoscendo il coefficiente di attrito dinamico possiamo calcolare la forza di attrito dalla formula
$F_a=F_vμ_D$
La reazione vincolare è la forza applicata dal piano d'appoggio al blocco. Nel punto A la reazione vincolare punta verso il centro del tratto circolare
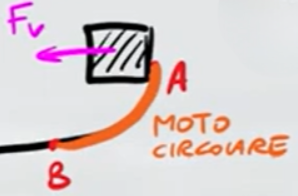
La forza che punta verso il centro del tratto circolare è la forza centripeta, siccome la reazione vincolare punta anch'essa verso il centro deve corrispondere alla forza centripeta del blocco.
$F_v=F_c$
Sostituiamo la forza con il secondo principio della dinamica $F=ma$ ottenendo
$F_v=ma_c=4,2N$
L'accelerazione centripeta l'abbiamo ricavata nella seconda domanda. Sostituendo nella formula mostrata all'inizio della terza domanda ricaviamo la forza di attrito nel punto A
$F_a=ma_cμ_D=0,84N$
QUARTA DOMANDA
Per poter ricavare l'accelerazione totale possiamo utilizzare il secondo principio della dinamica
$F_{tot}=ma_{tot}$
$a_{tot}=\frac{F_{tot}}{m}$
Per poter calcolare la forza totale dobbiamo sommare tutte le forze che agiscono sul blocco nel punto A
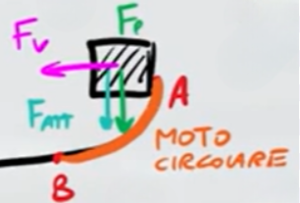
Dove $F_v$ è la reazione vincolare (uguale alla forza centripeta). La forza di attrito è opposta al moto del blocco, se il moto del blocco è verso l'alto la forza di attrito punta verso il basso coma la forza peso $F_p$.
Per poter calcolare la forza totale dobbiamo applicare il teorema di Pitagora tra le forze sull'asse Y (attrito e forze peso) e le forze sull'asse X (reazione vincolare)
$F_{tot}=\sqrt{(F_{att}+F_p)^2+F_{v}^2}$
La reazione vincolare e la forza di attrito le abbiamo ricavate nella terza domanda, la forza peso invece è:
$F_p=mg=2,94N$
Sostituendo i dati otteniamo
$F_{tot}=5,7N$
Dall'equazione mostrata all'inizio della domanda ricaviamo l'accelerazione totale
$a_{tot}=\frac{F_{tot}}{m}=19$ $m/s^2$
