Per poter superare il giro della morte, la macchinina deve raggiungere una velocità minima necessaria a bilanciare il peso.
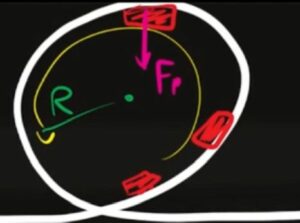
All'interno del giro, l'unica forza in grado di bilanciare il peso è la forza centripeta, cioè quella forza che spinge la macchinina a continuare il suo moto circolare attorno al giro.
La formula della forza centripeta è:
$F_C=m\frac{v^2}{r}$
Uguagliando questa forza alla forza peso possiamo ricavare la velocità minima
$m\frac{v^2}{r}=mg$
$v^2=gr$
$v=\sqrt{gr}=1$ $m/s$
ENERGIA CINETICA
Questa velocità ricavata rappresenta la velocità finale della macchinina. Supponiamo che la macchinina parta da ferma per poi scivolare dal piano inclinato per guadagnare velocità, in questo modo la velocità inziale della macchinina è 0
$v_i=0$
Sostituendo queste due velocità nella formula dell'energia cinetica totale otteniamo
$ΔE=\frac{1}{2}mv^2-\frac{1}{2}mv_{i}^2$
$ΔE=\frac{1}{2}mgr$
ENERGIA POTENZIALE
Nel problema abbiamo posto come punto finale il punto in cui la forza centripeta della macchinina bilancia completamente la forza peso, cioè il punto più alto del giro. L'altezza del punto più alto è semplicemente la lunghezza del diametro del cerchio, cioè $2R$
$h_f=2R=0,2m$
L'altezza iniziale del piano inclinato, invece, è l'incognita che dobbiamo ricavare.
La formula dell'energia potenziale totale è:
$ΔU=U_f-U_i$
Sostituendo l'energia potenziale finale ed inziale con la formula dell'energia potenziale gravitazionale otteniamo:
$ΔU=2mgR-mgh_i$
LAVORO TOTALE
Per ricavare l'altezza inziale dobbiamo inserire l'energia cinetica e l'energia potenziale ricavata all'interno della formula della conservazione del lavoro
$ΔE+ΔU=0$
$\frac{1}{2}mgr+2mgR-mgh_i=0$
Risolvendo questa equazione possiamo ricavare $h_i$
$mgh_i=\frac{1}{2}mgr+2mgR$
$h_i=\frac{1}{2}r+2R=\frac{5}{2}R$
Sostituendo il valore del raggio del giro $R$ otteniamo
$h_i=0,25m=25cm$
