ENERGIA CINETICA
Per poter risolvere questo problema dobbiamo utilizzare sempre la conservazione del lavoro
$L=0$
Quindi dobbiamo scrivere che la somma di tutte le energie è uguale a 0
$ΔE+ΔU=0$
Dove $ΔE$ è la differenza tra energia cinetica finale ed energia cinetica inziale ed è:
$ΔE=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2$
Il sasso parte da fermo per poi essere lanciato in aria dalla molla. Quindi l'energia cinetica inziale è 0
$ΔE=\frac{1}{2}mv_{f}^2$
ENERGIA POTENZIALE
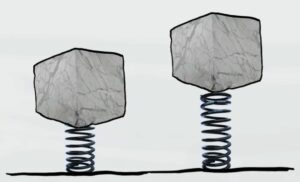
In questo problema però il sasso è lanciato verso l'alto, quindi oltre l'energia potenziale della molla che lo tira verso l'alto è presenta anche l'energia potenziale data dal peso del sasso che lo tira verso il basso.
La molla trasferisce la sua energia potenziale elastica al sasso sottoforma di energia cinetica lanciandolo in aria. Successivamente il sasso converte la sua energia cinetica in energia potenziale per poi cadere. Quindi l'energia potenziale totale del sasso è data dalla somma delle due energie
$ΔU=mgh_f-mgh_i+\frac{1}{2}kx_{f}^2-\frac{1}{2}kx_{i}^2$
Dopo aver lanciato il sasso la molla, da che era compressa, ritorna nella sua posizione iniziale. Di conseguenza la compressione finale è uguale a 0 ($x_f=0$)
Quindi anche l'energia potenziale elastica finale è uguale a 0
$ΔU=mgh_f-mgh_i-\frac{1}{2}kx_{i}^2$
Inoltre nel nostro sistema di riferimento il sasso si trova ad un altezza iniziale $h_i=0$
$ΔU=mgh_f-\frac{1}{2}kx_{i}^2$
LAVORO TOTALE
Sostituendo l'energia cinetica totale e l'energia potenziale ricavata nella formula della conservazione del lavoro
$\frac{1}{2}mv_{f}^2+mgh_f-\frac{1}{2}kx_{i}^2=0$
Da questa equazione possiamo ricavare l'incognita della velocità finale $v_f$
$\frac{1}{2}mv_{f}^2=-mgh_f+\frac{1}{2}kx_{i}^2$
$v_{f}^2=\frac{2}{m}(-mgh_f+\frac{1}{2}kx_{i}^2)$
Applicando la radice quadrata ad entrambi i membri otteniamo
$v_f=\sqrt{\frac{2}{m}(-mgh_f+\frac{1}{2}kx_{i}^2)}=0,535$ $m/s$
