Il lavoro non conservativo rappresenta l'energia totale di un corpo, cioè la somma tra energia cinetica e le varie energie potenziali.
$L=ΔE+ΔU$
In un sistema isolato (cioè dove non sono presenti forze esterne) vale la legge della conservazione dell'energia, cioè
$ΔE+ΔU=0$
Dove i Δ indicano le variazioni dell'energia, cioè la differenza tra energia finale ed energia inziale
$E_f-E_i+U_f-U_i=0$
SISTEMA NON ISOLATO
Se invece il sistema non è isolato ed è presente attrito, il lavoro non conservativo sarà proprio il lavoro della forza di attrito
$L=FΔx=μNΔx$
Dove μ è il coefficiente di attrito e $N$ la reazione vincolare del corpo. Quindi in un sistema non isolato il lavoro dell'attrito rappresenta la somma totale dell'energia
$ΔE+ΔU=μNΔx$
Questo perché l'attrito è una forma di dissipazione dell'energia. Se non è presente attrito il lavoro vale 0 perché tutta l'energia cinetica viene convertita in energia potenziale senza dispersioni. Se invece è presente attrito una parte di energia si disperde sottoforma di calore.
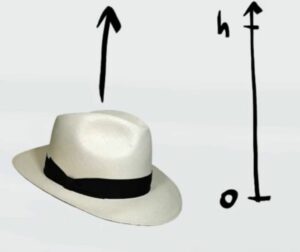
- Esercizio 1 (moto verticale)
Un cappello viene lanciato verso l'alto con una velocità inziale $v_i=7,85$ $m/s$ in assenza di attrito. Qual è l'altezza massima raggiunta dal cappello durante il lancio?
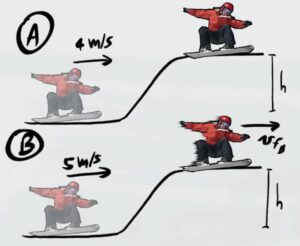
- Esercizio 2 (percorso in salita)
Un ragazzo su uno snowboard deve affrontare un percorso in salita. La prima volta raggiunge il livello superiore con una velocità inziale $v_i=4$ $m/s$ e appena arriva al punto più alto si ferma. Nel secondo tentativo parte con una velocità inziale $v_i=5$ $m/s$ e quando raggiunge il livello superiore continua a muoversi in avanti.
Qual è la velocità finale del ragazzo nel secondo tentativo?
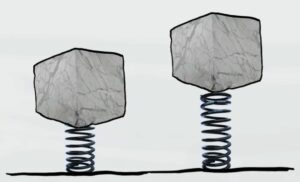
- Esercizio 3 (molla verticale)
Un sasso di massa $m=1,7kg$ è poggiato su una molla verticale di costante elastica $k=955$ $N/m$ e ne causa una compressione di 4,6 centimetri. La molla reagisce al peso del sasso e si allunga fino alla lunghezza di riposo lanciando il sasso verso l'alto. Qual è la velocità del sasso dopo il lancio?
- Esercizio 4 (molla orizzontale)
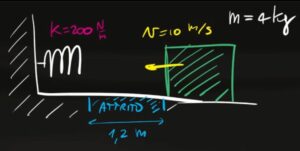
Un bocco di massa $m=4kg$ va verso una molla di costante elastica $k=200$ $N/m$ ad una velocità inziale $v=10$ $m/s$. Nel piano tratteggiato in blu, lungo 1,2 metri, è presente attrito dinamico con coefficiente $μ_D=0,1$. Di quanto si comprime la molla dopo l'urto del blocco.
- Esercizio 5 (doppia energia potenziale)
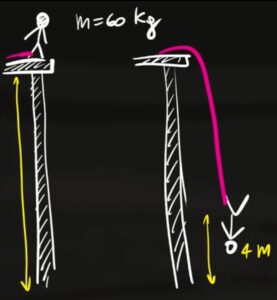
Una persona di massa $m=60kg$ mentre fa Bungee Jumping salta da un ponte alto 30 metri tenuto da una corda elastica. Dopo la caduta la persona si trova a 4 metri di altezza dal suolo. La corda elastica agisce come una molla, calcola la sua costante elastica.
- Esercizio 6 (piano inclinato + moto circolare)
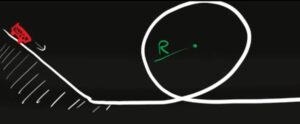
Un bambino gioca con le macchinine in una pista in cui è presente un giro della morte di raggio $r=10cm$. Prima di poter fare il giro la macchinina fa un percorso in discesa per guadagnare energia potenziale e per poter affrontare il giro. Quanto deve essere alto il percorso in discesa per poter effettuare il giro della morte?
- Esercizio 7 (molla + moto circolare)
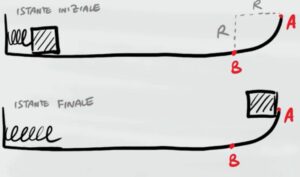
Un blocco di massa $m=0,3kg$ è appoggiato su un piano composto da un tratto lineare inziale e da un tratto circolare finale di raggio $R=0,8m$. Il blocco all'inizio viene spinto da una molla compressa di 0,25 metri e di costante elastica $k=150$ $N/m$. Su tutto il piano è presente attrito dinamico con coefficiente $μ_D=0,2$.
Il tratto circolare va dal punto B al punto A come mostrato in figura e la velocità del blocco nel punto A è $v=3,35$ $m/s$
a) Qual è il lavoro totale dell'attrito?
b) Qual è l'accelerazione centripeta del blocco nel punto A?
c) Qual è la forza di attrito nel punto A?
d) Calcola l'accelerazione totale nel punto A
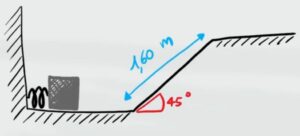
- Esercizio 8 (molla + piano inclinato)
Un corpo di massa $m=0,8kg$ deve percorrere un piano inclinato di 45° e lungo 1,6 metri. Per poterlo percorre viene spinto da una molla di costante elastica $k=500 N/m$ e compressa di $Δx=0,2m$.
Il blocco riesce ad arrivare in cima al piano inclinato? Se si, con quale velocità? Se no, a quale altezza si ferma?