Dato il grafico forza-spostamento diviso in 3 regioni
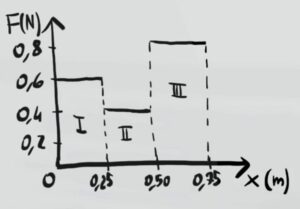
Possiamo calcolare il lavoro da $x_i=0,15m$ a $x_f=0.6m$ dobbiamo dividere il percorso in più tratti e sommarli. Questo perché tra un tratto e l'altro varia la forza ma per calcolare il lavoro, la forza deve essere costante.
$L=FΔx$
Dove $Δx$ è la variazione di spostamento
$Δx=x_f-x_i$
Nel primo tratto la forza vale $F=0,6N$ e lo spostamento va da $x_i=0,15 m$ a $x=0,25 m$. Il lavoro quindi è uguale a
$L_1=0,6\cdot (0,25-0,15)=0,06J$
Nel secondo tratto la forza vale $F=0,4N$ e lo spostamento va da $x_i=0,25m$ a $x=0,5m$.
$L_2=0,4\cdot (0,5-0,25)=0,1J$
Nel terzo tratto la forza vale $F=0,8N$ e lo spostamento va da $x_i=0,5m$ fino al tratto finale $x_f=0,6m$
$L_3=0,8\cdot (0,6-0,5)=0,08J$
Il lavoro totale del tratto è la somma di questi tre lavori
$L=L_1+L_2+L_3=0,24J$
