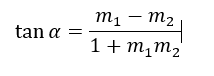La retta ha equazione:
![]()
In cui m è il coefficiente angolare della retta (indica quanto la retta è inclinata e se è uguale ad 1 l’angolo di inclinazione è 45°) e q il punto di intersezione con l’asse y.
Immagine di una retta sul piano cartesiano:
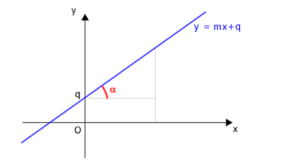
L’angolo di inclinazione si può ricavare considerando una parte della retta che forma un triangolo rettangolo in cui base a altezza sono dati da:
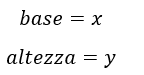
Usando le formule trigonometriche per i triangoli rettangoli ricaviamo l’equazione per poter trovare alfa:
![]()
Ricaviamo alfa usando le operazioni trigonometriche inverse
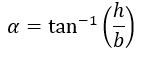
Sostituendo la base e l’altezza del triangolo con x e y otteniamo:
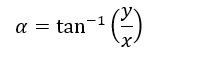
Sostituendo y con y = mx + q otteniamo:
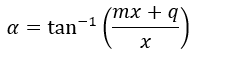
Per poter ricavare i punti di intersezione tra due rette basta porre uguali le due equazioni delle rette.
Abbiamo le 2 equazioni delle rette:
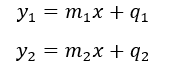
Poniamole uguali tra loro:
![]()
Risolviamo per x ottenendo:
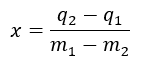
Per poter poi trovare il valore y del punto di intersezione basta sostituire il valore trovato di x in una delle due equazioni delle rette.
Due rette si dicono perpendicolari tra loro quando il loro angolo di intersezione è di 90°.
Immagine di due rette perpendicolari:
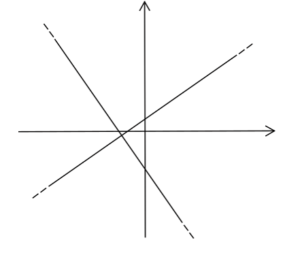
Per poter ricavare l’angolo di intersezione tra due rette bisogna usare lo stesso ragionamento che abbiamo usato per ricavare l’angolo di inclinazione di una retta ottenendo: