La parabola è descritta da un’equazione di secondo grado di questo tipo:
![]()
Più a è grande più la parabola sarà stretta verso l’origine, mentre più a è piccola più la parabola sarà allargata verso l’asse x.
Più b è grande e più il centro della parabola sarà distante dall’origine.
Più c è grande e più la parabola sarà in alto o in basso nell’asse y.
Inoltre la parabola viene definita concava se a > 0 (cioè se la parabola si trova sull’asse positivo delle y) o convessa se a < 0 (cioè se la parabola si trova sull’asse y negativa).
Immagine di una parabola:
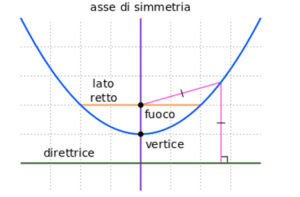
Per poter trovare i punti di intersezione tra due parabole basta porre le due equazioni delle parabole uguali e risolvere l’equazione di secondo grado per l’incognita x.
Le formule per ricavare vertice, fuoco, asse di simmetria e direttrice sono le seguenti:
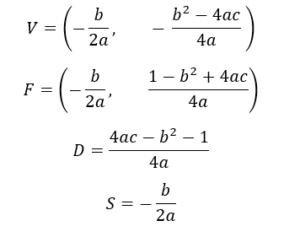
INTERSEZIONE DI UNA PARABOLA CON UNA RETTA TANGENTE:
La prima cosa da fare quando si considera un'intersezione è porre le due funzioni uguali:
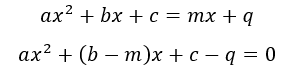
Da questa equazione di secondo grado ricaviamo il delta e lo poniamo uguale a 0 (perché la retta è tangente, quindi il punto di intersezione è solo uno) ottenendo:
![]()
Calcoliamo il quadrato di b – m ottenendo un equazione completa:
![]()
Si può fare lo stesso procedimento se si vuole trovare il punto di intersezione di due parabole tangenti (cioè che si intersecano in un punto solo) oppure tra una parabola ed un qualsiasi altro luogo geometrico.
