Per poter calcolare i massimi di interferenza dobbiamo trovare tutti i coefficienti $n$ di $λ/2$ usando la formula delle interferenze tra onde sonore
$|r_A-r_B|=n\frac{λ}{2}$
Siccome la persona sta girando intorno alla sorgente A, la distanza tra la persona e la sorgente A rimane la stessa (cioè il raggio della circonferenza) ma varia la distanza tra la persona e la sorgente B.
Indichiamo sulla circonferenza due punti P e Q dove P è il punto sulla circonferenza più lontano dalla sorgente B mentre Q è il più vicino alla sorgente B
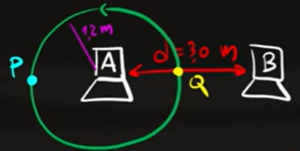
Nel punto Q la distanza tra la persona è la differenza tra la distanza $d$ (in rosso) e il raggio della circonferenza (1,2 metri)
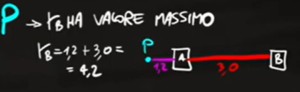
Quindi
$r_B=r_A+d=1,2+3$
$r_B=4,2m$
Il punto Q si trova tra il raggio della circonferenza e la distanza $d$, quindi la sua distanza dalla sorgente $r_B$ è data dalla differenza tra la distanza $d$ e il raggio (1,2 metri)

$r_B=d-r=3-1,2$
$r_B=1,8m$
Quindi abbiamo due valori della distanza $r_B$
$r_B(max)=4,2m$
$r_B(min)=1,8m$
Quindi possiamo calcolare il minimo e il massimo di $n$
$|r_A-r_B|=n\frac{λ}{2}$
$n=\frac{2}{λ}|r_A-r_B|$
Per calcolare la lunghezza d'onda delle onde possiamo utilizzare la formula del moto delle onde (sapendo che $v=343$ $m/s$)
$v=λf$
$λ=\frac{v}{f}=0,78m$
Ora che abbiamo tutti i dati possiamo calcolare i due valori estremi di $n$
$r_B=4,2m → n=7,7$
$r_B=1,8m → n=1,5$
Siccome stiamo considerando tutte le interferenze complete, consideriamo i due valori estremi interi di $n$
$n=1$, $n=7$
Quindi mentre la persona va da $P$ a $Q$ passa per 7 punti di interferenza e poi passa per altri 7 quando va da $Q$ a $P$
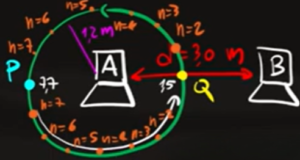
In questo disegno vengono rappresentati tutti i punti di interferenze lungo la circonferenza.
Il problema ci chiede quanti MASSIMI di interferenza incontra la persona, quindi dobbiamo contare tutte le interferenze costruttive ($n$ pari)
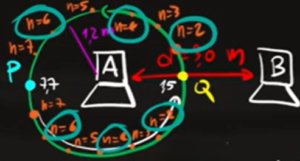
Contando tutti gli $n$ pari presenti lungo la circonferenza, otteniamo che la persona incontra 6 interferenze costruttive per ogni giro
