Per risolvere questo problema dobbiamo trovare il coefficiente che moltiplica $λ/2$. Infatti è presente un interferenza totale solo nei punti in cui il coefficiente risulta essere un numero intero. Per ricavarlo possiamo usare la formula per le onde sonore
$|r_A-r_B|=n\frac{λ}{2}$
Per prima cosa calcoliamo la distanza dalla sorgente B ($r_B$)
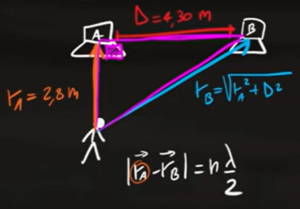
Come si vede dall'immagine, la distanza $r_B$ è l'ipotenusa del triangolo rettangolo i cui cateti sono $r_A$ e $D$. Quindi, per il teorema di Pitagora, la distanza $r_B$ è:
$r_B=\sqrt{r_{A}^2+D^2}=5,13m$
Ora che abbiamo le due distanze possiamo ricavare il coefficiente $n$ dall'equazione mostrata prima
$|r_A-r_B|=n\frac{λ}{2}$
$n=\frac{2}{λ}|r_A-r_B|$
Dai dati non ci viene fornita la lunghezza d'onda, ma possiamo ricavarla dall'equazione della velocità delle onde
$v=λf$
Dove $f=220Hz$ e $v=343$ $m/s$ (velocità del suono). Quindi la lunghezza d'onda è:
$λ=\frac{v}{f}=1,56m$
Svolgendo i calcoli per $n$ otteniamo:
$n=\frac{2}{λ}|r_A-r_B|=3$
Siccome $n$ è un numero intero, nel punto in cui vi trovate è presente un'interferenza totale e siccome è anche un numero dispari si tratta di un'interferenza distruttiva.
