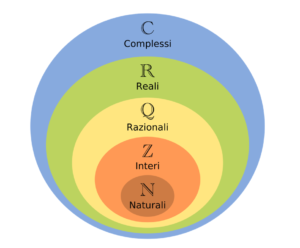
Gli insiemi numerici sono insiemi infiniti, sono costituiti solo da numeri e sono differenziati in ordine crescente (anche se sono infiniti ci sono insiemi più grandi di altri perché contengono i loro stessi elementi più un altro numero infinito di elementi):
- Insieme dei numeri naturali che contiene tutti i numeri interi positivi.
- Insiemi dei numeri interi che contiene tutti i numeri naturali, in più contiene anche tutti i numeri interi negativi.
- Insieme dei numeri razionali che contiene tutti i numeri interi, in più contiene anche i numeri periodici e i numeri decimali razionali.
- Insieme dei numeri reali che contiene tutti i numeri razionali, in più contiene anche tutti i numeri irrazionali.
- Insieme dei numeri complessi che contiene tutti i multipli della radice di (-1), un numero complesso viene rappresentato in questo modo:
![]()
In cui a, b sono due numeri reali e i la radice di (-1)
Gli insiemi matematici sono infiniti, infatti si possono creare insiemi matematici prendendo, per esempio, tutti i numeri maggiori di 3 oppure tutti i numeri minori di 7.
Un esempio di insieme:
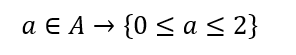
Questa scritta significa: “a fa parte dell’insieme A se e solo se a è compresa tra 0 e 2”.
Infatti in matematica viene usato un proprio linguaggio per descrivere gli insiemi.
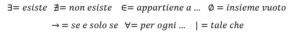
Per esempio la scritta:

Vuole dire: “per ogni x appartenente ad A esiste una a tale che b sia maggiore di 0”.