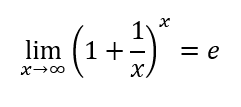I limiti vengono scritti in questo modo:
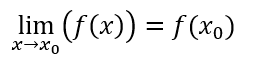
In cui f(x) è la funzione scelta e x0 è il valore scelto
Per esempio calcoliamo il seguente limite:
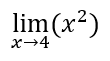
Basta sostituire la x con il valore scelto ottenendo:
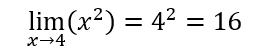
FORME DI INDETERMINAZIONE
Ci sono alcuni limiti che non si possono calcolare semplicemente sostituendo x con il termine scelto perché danno come risultato una forma di indeterminazione che sono le seguenti:
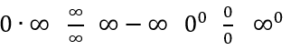
Se il risultato di un limite è una forma di indeterminazione ci sono due metodi per risolverlo:
1) La Regola di De L’Hopital (applicabile solo alle funzioni frazionarie) dice che, se il risultato del limite è una forma di indeterminazione, si può applicare la derivata sia al denominatore che al nominatore finché non si arriva ad un risultato determinato.
Esempio:
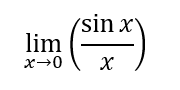
Se sostituissimo x con 0 otterremmo una forma di indeterminazione, quindi applichiamo ambo i membri la derivata ottenendo:
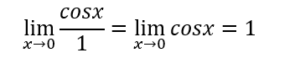
- La gerarchia degli infiniti, si può applicare solo ai limiti che tendono a infinito, questa regola consiste nello scegliere, tra i membri della funzione, quello più grande (cioè quello che considerato come funzione cresce più velocemente).
Esempio:
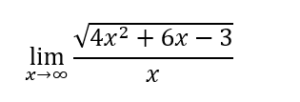
Nel nominatore scegliamo il termine più grande ottenendo:
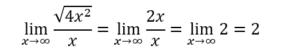
Se in un limite ci sono termini diversi per cui non si capisce quale sia il più grande basta dividerli tra loro e applicare la regola di De L’Hopital.
Esempio:
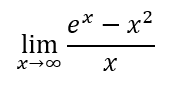
Non sapendo quale sia il termine più grande nel denominatore li dividiamo tra loro in questo modo:
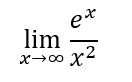
Applichiamo la regola per ottenere:
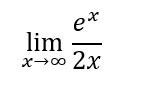
Siccome il risultato è ancora indeterminato applichiamo di nuovo la regola:
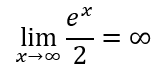
Quindi da qui possiamo concludere che è più grande di quindi possiamo ora risolvere il limite iniziale:
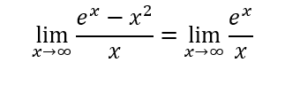
Dal limite che abbiamo calcolato precedentemente possiamo concludere che il limite è infinito.
LIMITI NEGATIVI
Alcuni limiti sono rappresentati in questo modo:
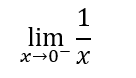
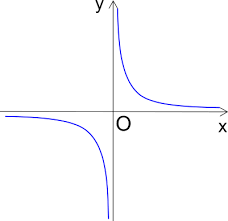
Quel meno posto all’apice dello 0 indica che si sta calcolando il limite di x che tende a 0 però dal lato negativo delle x. Cioè un numero poco più piccolo di 0 e dal grafico della funzione 1/x si può vedere che per x che tende a 0 dal lato delle x negative, il limite viene negativo
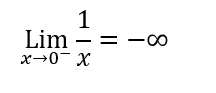
NUMERO DI NEPERO
L’ultima notazione sui limiti è il numero di Nepero che proviene dal seguente limite: