- Esercizio 1 (attrito statico)
La macchina è ferma se la forza di attrito riesce ad equilibrare la forza della spinta

Quindi la forza di attrito deve essere uguale e contraria alla forza della spinta
$F_a=-260N$
Il coefficiente di attrito statico si potrebbe ricavare dalla formula della forza di attrito massima
$F_s=μ_s\cdot N$
Ma in questo esercizio abbiamo ricavato la forza di attrito statico minima per mantenere l'equilibrio ed è impossibile stabilire da questi dati se la forza è massima. Quindi non possiamo ricavare il coefficiente di attrito statico.
- Esercizio 2 (attrito statico)
Per prima cosa dobbiamo considerare tutte le forze che agiscono sulla scatola: forza peso, reazione vincolare e forza di attrito. Siccome stiamo considerando un piano inclinato dobbiamo scomporre il peso nelle sue due componenti
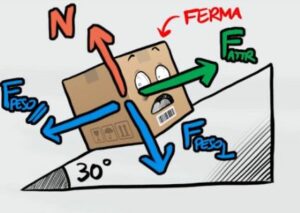
Dal grafico si può vedere che l'unica forza che si oppone all'attrito (colorato in verde) è la forza peso parallela.
$F_a=mgsin(30°)$
$F_a=15kg\cdot 9,81N/kg \cdot sin(30)°=74N$
- Esercizio 3 (attrito statico)
La fune crea un angolo di 60°, quindi possiamo scomporre la tensione nelle due componenti x e y
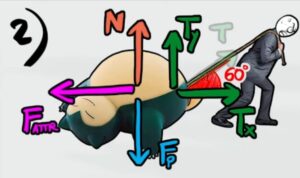
Calcoliamo le due componenti
$T_x=Tcos(60°)=100N$
$T_y=Tsin(60°)=173,2N$
Per poter stabilire se il corpo si muove o no dobbiamo capire se la forza che si oppone all'attrito (cioè $T_x$) riesce a superare l'attrito
$T_x>F_a$
RICAVARE L'ATTRITO
Per calcolare la forza di attrito massima usiamo la formula
$F_a=μ_SN$
Per ricavare la reazione vincolare dobbiamo scrivere l'equilibrio delle forze y. Cioè, siccome il corpo non si sta muovendo in alto o in basso possiamo affermare che la somma di tutte le forze che puntano verso l'alto (segno positivo) e tutte le forze che puntano verso il basso (segno negativo) è uguale a 0.
$N+T_y-F_p=0$
Da cui ricaviamo
$N=F_p-T_y=612N$
Sapendo il coefficiente di attrito statico possiamo calcolare la forza massima
$F_a=μ_SN=0,4\cdot 612N=245N$
SOLUZIONE
La tensione x vale 100N mentre la forza di attrito massima vale 245N. Dato che la forza di attrito è maggiore della forza della fune, il corpo non si muove.
- Esercizio 4 (attrito dinamico)
Avendo come dato la massa dell'armadio e il coefficiente di attrito dinamico. Possiamo calcolare la forza con la formula
$F_a=μ_DN$
L'armadio non si muove né in basso e né in alto quindi possiamo scrivere l'equilibrio delle forze sull'asse y (tutte le forze che puntano in alto o in basso)
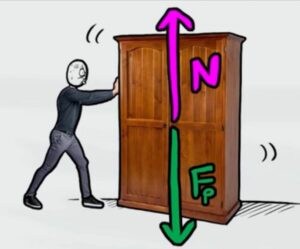
$N-F_p=0$
Da qui ricaviamo la reazione vincolare sapendo che il peso è mg
$N=mg=196,2N$
Inserendo la reazione vincolare nella formula inziale ricaviamo
$F_a=μ_DN=78N$
- Esercizio 5 (attrito volvente)
La formula per la forza di attrito volvente è
$F_v=\frac{N\cdot μ_v}{r}$
La ruota non si muove né in basso e né in alto quindi la reazione vincolare e il peso si bilanciano tra loro
$N=P=mg$
$N=50kg\cdot 9,81N/kg=490,5N$
Ora che abbiamo tutti i dati possiamo calcolare la forza di attrito volvente
$F_v=9,81N$
- Esercizio 6 (attrito volvente)
Dato che la sfera si trova su un piano inclinato, dobbiamo dividere la sua forza peso nelle due componenti
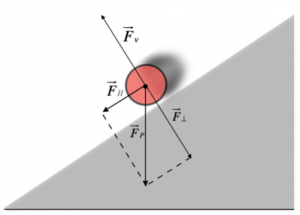
Ora calcoliamo le due componenti (x=parallela, y=perpendicolare)
$F_x=mgsin(10°)=3,4N$
$F_y=mgcos(10°)=19,3N$
Il corpo non si muove lungo la direzione y, quindi la reazione vincolare deve essere bilanciata dal peso perpendicolare (corrisponde alla componente y)
$N=F_y=19,3N$
Ora possiamo mettere tutto nella formula della forza di attrito volvente
$F_v=\frac{μ_vN}{r}=0,39N$
