Poniamo che la distanza tra il centro della Terra e il punto in cui le due accelerazioni gravitazionali si annullano sia $x$. In questo modo la distanza tra questo punto e il centro della Luna è $d-x$ dove $d$ è la distanza tra il centro della Terra e quello della Luna
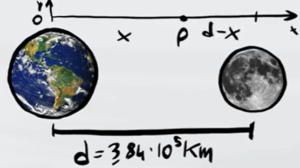
In questo modo sappiamo che l'accelerazione gravitazionale terrestre nel punto P è dato dalla distanza $x$
$g_t=G\frac{m_t}{x^2}$
Per la Luna vale la stessa formula con distanza $d-x$
$g_L=-G\frac{m_L}{(d-x)^2}$
Il meno va messo perché l'accelerazione gravitazionale lunare, rispetto al punto, ha verso opposto di quella terrestre.
Nel punto P le due accelerazioni gravitazionali si annullano, quindi la loro somma deve fare 0
$G\frac{m_t}{x^2}-G\frac{m_L}{(d-x)^2}=0$
Semplifichiamo ad entrambi i lati la costante $G$
$\frac{m_t}{x^2}-\frac{m_L}{(d-x)^2}=0$
Da questa equazione possiamo ricavare la distanza tra il punto P e il centro della Terra ($x$).
$\frac{m_t}{x^2}=\frac{m_L}{(d-x)^2}$
Per farlo, giriamo le due frazioni elevandole entrambe a (-1)
$\frac{x^2}{m_t}=\frac{(d-x)^2}{m_L}$
Espandiamo il quadrato di binomio
$\frac{x^2}{m_t}=\frac{d^2+x^2-2dx}{m_L}$
Applichiamo la moltiplicazione incrociata per togliere i denominatori
$x^2m_L=(d^2+x^2-2dx)m_t$
$x^2m_L=d^2m_t+x^2m_t-2dxm_t$
Portiamo tutto a sinistra dell'equazione e raccogliamo i termini in $x$
$x^2(m_L-m_t)+x(2dm_t)-d^2m_t=0$
Per risolvere questa equazione di secondo grado, basta usare le formula risolutiva
$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$
Dove a,b,c sono:
$a=m_L-m_t$
$b=2dm_t$
$c=-d^2m_t$
Sostituendo nella formula risolutiva otteniamo:
$x=\frac{-2dm_t\pm \sqrt{4d^2m_{t}^2-4(m_L-m_t)(-d^2m_t)}}{2(m_L-m_t)}$
$x=\frac{-2dm_t\pm \sqrt{4d^2m_{t}^2+4(m_L-m_t)(d^2m_t)}}{2(m_L-m_t)}$
Sostituendo i dati otteniamo:
$x=3,15\cdot 10^8m=315.000km$
Questa è la distanza tra il punto e la Terra, per trovare la distanza tra il punto e la Luna basta fare $d_x$
$d-x=384.000km-315.000km=69.000km$
