FORZA TOTALE SULLA TERRA
Guardando l'immagine possiamo vedere che la forza di attrazione tra la Terra e la Luna e tra la Terra e il Sole hanno stesso verso e direzione, quindi basta sommare queste due forze per trovare la forza totale agente sulla Terra
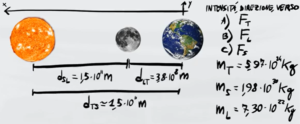
$F_t=F_{luna-terra}+F_{terra-sole}$
Le due forze si possono calcolare con la legge di Newton conoscendo le masse e le distanze tra i corpi:
$F_{lt}=G\frac{m_t\cdot m_l}{d_{lt}^2}$
$F_{ts}=G\frac{m_t\cdot m_s}{d_{ts}^2}$
Sostituendo queste due espressioni otteniamo:
$F_t=G\frac{m_t\cdot m_l}{d_{lt}^2}+G\frac{m_t\cdot m_s}{d_{ts}^2}$
Per semplificare i calcoli possiamo anche raccogliere i termini in comune tra le due frazioni
$F_t=Gm_t(\frac{m_l}{d_{lt}^2}+\frac{m_s}{d_{ts}^2})$
$F_t=3,56\cdot 10^{22}N$
FORZA TOTALE SUL SOLE
La forza di attrazione tra il Sole e la Luna e tra il Sole e la Terra hanno lo stesso verso, quindi anche in questo caso la forza totale è la somma di queste due forze gravitazionali
$F_s=F_{sole-luna}+F_{terra-sole}$
Sostituendo le due forze con la legge di Newton otteniamo:
$F_{sl}=G\frac{m_s\cdot m_l}{d_{sl}^2}$
$F_{ts}=G\frac{m_s\cdot m_t}{d_{ts}^2}$
Quindi la forza totale agente sul Sole diventa:
$F_s=G\frac{m_s\cdot m_l}{d_{sl}^2}+G\frac{m_s\cdot m_t}{d_{ts}^2}$
Raccogliamo i termini comuni tra le due frazioni per semplificare i calcoli
$F_s=Gm_s(\frac{m_l}{d_{sl}^2}+\frac{m_t}{d_{ts}^2})$
$F_s=3,58\cdot 10^{22}N$
FORZA TOTALE SULLA LUNA
Come si vede nell'immagine, la Luna sta in mezzo ai due corpi. Mentre la forza di attrazione tra la luna e il Sole va verso sinistra, la forza di attrazione tra la Luna e la Terra va verso destra, quindi la forza totale agente sulla Luna è la differenza tra queste due forze di verso opposto
$F_l=F_{luna-terra}-F_{sole-luna}$
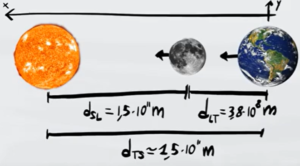
Scegliamo come positiva la forza che va verso destra (luna-terra) e come negativa la forza che va verso sinistra (sole-luna). Sostituiamo le due forze con la legge di Newton
$F_{lt}=G\frac{m_l\cdot m_t}{d_{lt}^2}$
$F_{sl}=G\frac{m_s\cdot m_l}{d_{sl}^2}$
Quindi la forza totale agente sulla Luna è:
$F_l=G\frac{m_l\cdot m_t}{d_{lt}^2}-G\frac{m_s\cdot m_l}{d_{sl}^2}$
Raccogliamo i termini comuni per semplificare l'espressione
$F_l=Gm_l(\frac{m_t}{d_{lt}^2}-\frac{m_s}{d_{sl}^2})$
