I corpi dotati di massa sono attratti tra di loro per la forza di gravità. La legge di Newton afferma che l'intensità di questa forza è inversamente proporzionale al quadrato della distanza tra i due corpi e direttamente proporzionale al prodotto delle due masse
$F_G=G\frac{m_1m_2}{r^2}$
Dove G è la costante di gravitazione universale
$G=6,674\cdot 10^{-11}Nm^2/kg^2$
In pratica la legge di Newton afferma che la forza di gravità aumenta se i due corpi si avvicinano tra di loro e dipende dalla massa di quest'ultimi.
Inoltre se consideriamo un'orbita quasi sferica di un pianeta o satellite di massa $m_1$, possiamo approssimare la forza di gravità alla forza centripeta
$rm_1ω^2=G\frac{m_1m_2}{r^2}$
$rω^2=G\frac{m_2}{r^2}$
Dove ω è la velocità angolare del pianeta o satellite in rotazione $m_2$ la massa del corpo attorno al quale orbita
ACCELERAZIONE GRAVITAZIONALE
Se consideriamo un corpo di massa $m$ che cade su un pianeta di massa $M$ con accelerazione $a$, la somma di tutte le forze che agiscono su di esso è dato dal secondo principio della dinamica
$F=ma$
Se sul corpo non agiscono altre forze oltre la forza gravitazionale, possiamo uguagliarla al secondo principio della dinamica
$F_G=G\frac{mM}{r^2}=ma$
$F_G=G\frac{M}{r^2}=a$
Questa accelerazione che abbiamo appena ricavato è l'accelerazione del corpo che cade sul pianeta di massa $M$ dove $r$ rappresenta il raggio del pianeta. Quindi l'accelerazione che abbiamo calcolato è l'accelerazione gravitazionale del pianeta (sulla terra vale $9,81$ $m/s^2$)
- Esercizio 1
Ti trovi ad una distanza $r=14.000km$ dal satellite Cerere di massa $m_c=8,7\cdot 10^{20}kg$. Quanto vale la forza gravitazionale tra te e Cerere?
(P.s: puoi usare un valore approssimato per la tua massa)
- Esercizio 2
Nella fase di luna Nuova la Terra, la Luna e il Sole sono allineati come in figura. Determina la forza gravitazionale totale agente su ognuno di loro
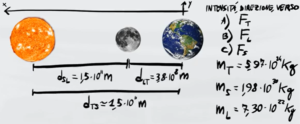
- Esercizio 3
Tre corpi di massa equivalente $m=6,75kg$ sono posti ai vertici di un triangolo equilatero. Se il lato del triangolo è $l=1,25m$ determina:
a) La forza gravitazionale risultante su ognuno dei tre corpi
b) La forza gravitazionale risultante se il lato del triangolo raddoppia
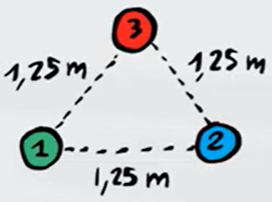
- Esercizio 4
L'accelerazione gravitazionale della Luna è circa $1/6$ di quella terrestre e il suo raggio è circa $1/4$ quello terrestre. Esprimi la massa della Luna in funzione della massa terrestre
- Esercizio 5
Un satellite artificiale sta orbitando attorno alla Terra e lentamente si allontana da quest'ultima. Calcola il periodo dell'orbita del satellite quando la distanza dal centro della terra è pari a 1 raggio terrestre e a 2 raggi terrestri.
(Il raggio della Terra è $r_T=6378km$ e la sua massa è $m_T=5,97\cdot 10^{24}kg$)
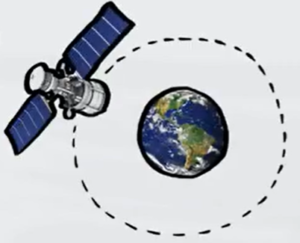
- Esercizio 6
La distanza media tra i centri della Terra e della Luna è $d=3,84\cdot 10^8m$. Sapendo che la massa della Terra è $m_T=5,97\cdot 10^{24}kg$ e la massa della Luna è $m_L=7,35\cdot 10^{22}kg$ determina il punto tra i due corpi in cui l'accelerazione gravitazionale è nulla
- Esercizio 7
Il pianeta Ida 243 possiede una propria luna chiamata Dactyl. Quanto vale la massa di Ida 243 sapendo che la distanza tra i centri dei due corpi celesti è $d=89km$ e il periodo di rivoluzione di Dactyl è $T=19h$?
