- Esercizio 1 (molla orizzontale)
Il problema ci da come dati la forza esterna che fa allungare la molla (30 N) e l'allungamento massimo (0,5 m). Quando la molla raggiunge l'allungamento massimo la forza elastica e la forza esterna si equivalgono.
$F_e=kΔx$
Dove $F_e$ sta per forza esterna. Da questa formula possiamo ricavare la costante elastica
$k=\frac{F_e}{Δx}=60 N/m$
- Esercizi 2 (molla orizzontale)
L'allungamento della molla indica la variazione di lunghezza. Cioè $Δx$ è la differenza tra la lunghezza totale della molla ($x$) e la lunghezza a riposo ($x_0$).
$F_e=k(x-x_0)$
Il problema ci chiede la lunghezza totale, quindi dobbiamo risolvere l'equazione per x
$\frac{F_e}{k}=x-x_0$
$x=\frac{F_e}{k}+x_0=0,22m$
- Esercizio 3 (due molle orizzontali)
Per prima cosa scriviamo le equazioni delle forze elastiche delle due molle a cui è applicata la stessa forza F di 5 N
$F=k_1Δx_1$
$F=k_2Δx_2$
Da queste equazioni possiamo ricavare le due costanti elastiche sapendo che le due $Δx$ valgono 0,1m e 0,2m
$k_1=\frac{F}{Δx_1}=100 N/m$
$k_2=\frac{F}{Δx_2}=50 N/m$
La relazione che lega forza elastica e allungamento delle molle è semplicemente l'equazione della forza elastica che ha come incognita l'allungamento delle molle
$F_1=100Δx_1$
$F_2=50Δx_2$
- Esercizio 4 (molla verticale)
Sulla molla in equilibrio sono applicate due forze, la forza elastica e la forza peso dell'oggetto attaccato.

In un sistema in equilibrio le due forze opposte sono uguali tra loro
$F_e=F_p$
In cui $F_p$ è la forza peso dell'oggetto attaccato e $F_e$ è la forza elastica della molla che si oppone al peso dell'oggetto. Sostituendo le due forze otteniamo
$kΔx=mg$
Da questa formula possiamo ricavare l'allungamento della molla
$Δx=\frac{mg}{k}≈0,01m$
- Esercizio 5 (due molle verticali)
Ogni molla si allunga fino a quando non è in equilibrio con la massa. Quindi possiamo scrivere che ognuna delle due molle è in equilibrio con il corpo appeso.
$mg=k_1Δx_1$
$mg=k_2Δx_2$
In questo modo possiamo ricavare gli allungamenti delle due molle
$Δx_1=\frac{mg}{k_1}=0,017m$
$Δx_2=\frac{mg}{k_2}=0,011m$
Per rispondere alla seconda domanda, dobbiamo considerare le due molle come un unica molla con costante elastica $k_0$ e con allungamento totale dato dagli allungamenti delle singole molle
$F_e=k_0(Δx_1+Δx_2)$
Questa molla è anch'essa in equilibrio con l'oggetto appeso
$mg=k_0(Δx_1+Δx_2)$
Risolvendo l'equazione possiamo ricavare k_0
$k_0=\frac{mg}{Δx_1+Δx_2}=700,7N/m$
- Esercizio 6 (molla su piano inclinato)
Per prima cosa disegniamo tutte le forze che agiscono sul corpo
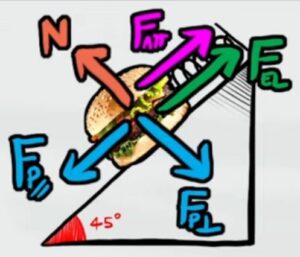
Dove Fp parallela è mgsin(45°) mentre Fp perpendicolare è mgcos(45°)
EQUILIBRI DELLE FORZE
Dalla foto possiamo scrivere l'equilibrio delle forze sapendo che sono uguali tutte le forze che sono opposte tra loro
EQUILIBRIO ASSE X →$mgsin(45°)=F_A+F_E$
EQUILIBRIO ASSE Y → $mgcos(45°)=N$
RICAVARE LA FORZA DI ATTRITO
Dove $F_A$ è la forza di attrito e $F_E$ è la forza elastica.
La forza di attrito la possiamo calcolare usando il coefficiente di attrito statico fornito dai dati
$F_A=μ_S\cdot N$
La reazione vincolare la ricaviamo dall'equilibrio sull'asse Y
$F_A=μ_S\cdot mgcos(45°)=2,77N$
RICAVARE LA FORZA ELASTICA
In questo modo possiamo ricavare la forza elastica tramite l'equilibrio sull'asse X
$mgsin(45°)=F_A+F_E$
Da questa equazione ricaviamo $F_E$
$F_E=mgsin(45°)-F_A=13,87N-2,77N$
$F_E=11,1N$
SOLUZIONE
Dalla formula della forza elastica
$F_E=kΔx$
Conosciamo la forza elastica e la costante elastica (ricavata dai dati del problema), quindi possiamo ricavare l'allungamento della molla
$Δx=\frac{F_E}{k}=0,28m$
