PAGINA DI TEORIA: Forza di Coulomb
La forza di Coulomb è la forza generata dall'interazione tra cariche elettriche e si calcola tramite la seguente formula:
$F=\frac{kq_1q_2}{r^2}$
Dove $q_1$ e $q_2$ sono le due cariche elettriche che interagiscono, $r$ è la loro distanza e $K$ è la costante elettrica, che si misura in questo modo
$k=\frac{1}{4πε_0ε_r}$
Dove $ε_0$ è la costante dielettrica del vuoto mentre $ε_r$ è la costante dielettrica del mezzo in cui i due corpi carichi si trovano. Se si trovano nel vuoto la costante elettrica si riduce a:
$k=\frac{1}{4πε_0}≈9\cdot 10^9$ $Nm^2/C^2$
- Esercizio 1
Calcola la forza elettrica generata dall'interazione di un protone ($q_1=1,6\cdot 10^{-19}C$) e di un elettrone nell'atomo di idrogeno, dove le due particelle si trovano a $r=1,2\cdot 10^{-10}m$
- Esercizio 2
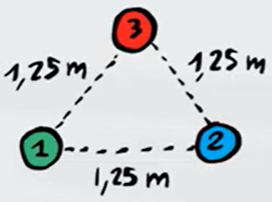
Tre corpi positivi di carica $Q=1$ $μC$ si trovano ai vertici di un triangolo equilatero di lato $l=1,25m$. Calcola la forza elettrica risultante agente sui tre corpi. La forza risultante è di attrazione o di repulsione?
- Esercizio 3
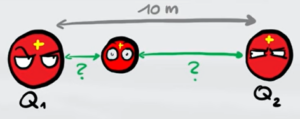
Due cariche elettrica $q_1=2$ $nC$ e $q_2=8$ $nC$ si trovano ad una distanza $r=10$ $m$ l'una dall'altra. Ad un certo punto viene inserita una terza carica elettrica in mezzo alle due cariche inziali e si arriva ad una posizione di equilibrio in cui la terza carica né viene respinta e né viene attratta. Calcola la distanza dalla prima carica a cui deve essere messa la carica 3 per far si che rimanga in uno stato di equilibrio
- Esercizio 4
Quattro protoni di carica $q=1,6\cdot 10^{-19}C$ si trovano ai vertici di un quadrato di lato $L=1m$. Sapendo che i protoni all'instante iniziale partono da fermi e negli istanti successivi si respingono tra di loro, calcola la loro velocità dopo $t=1s$
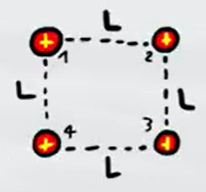
- Esercizio 5
La somma di due cariche elettriche è $Q_{TOT}=1$ $nC$ e la loro forza di Coulomb risulta $F=3$ $N$ a $r=2m$ di distanza l'una dall'altra. Determina il valore delle due cariche elettriche.
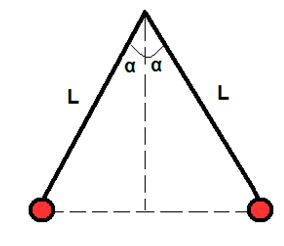
- Esercizio 6
Due sfere hanno la stessa carica elettrica e la stessa massa e si trovano ciascuna su un filo di lunghezza $L$ e oscillano in maniera simmetrica. Arrivati ad un certo punto entrambe le sfere si trovano in un punto di equilibrio ad un angolo $2α$ rispetto all'asse Y. Trova un equazione che determini la carica delle sfere in funzione dell'angolo $α$