Consideriamo le forze che agiscono sulle due sferette, la forza elettrica tra le due sfere, la forza peso e la tensione. La forza peso e la forza elettrica possiamo determinarle dai principi della dinamica e dalla formula della forza di Coulomb
$P=mg$
$F=\frac{Kq^2}{r^2}$
Dalla figura del problema possiamo notare che dividendo l'angolo in due parti uguali si ottengono due triangoli rettangoli di base $r/2$ e di ipotenusa $L$ dove $r$ è la distanza tra le due sferette
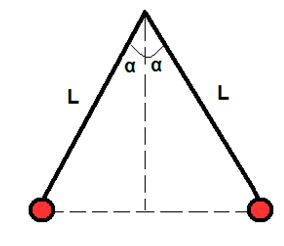
Utilizzando le formule trigonometriche del triangolo rettangolo possiamo ricavare la distanza tra le due sferette
$Lsin(α)=\frac{r}{2}$
NOTA: Per ricavare la base del triangolo rettangolo dobbiamo utilizzare il seno dell'angolo perché la base si oppone all'angolo stesso.
Da questa equazione possiamo ricavare la distanza $r$
$r=2Lsin(α)$
Quindi la forza di Coulomb diventa:
$F=\frac{Kq^2}{4L^2sin^2(α)}$
Le sfere si trovano in equilibrio, quindi dobbiamo scrivere un equazione per l'equilibrio sull'asse X e una per l'equilibrio sull'asse Y
EQUILIBRIO ASSE Y
Sull'asse Y ci sono le uniche due forze verticali: la componente verticale della tensione e la forza peso delle sfere
$T_y-P=0$
Sostituiamo i due valori e otteniamo
$Tcos(α)-mg=0$
Da questa equazione possiamo ricavare la tensione del filo
$T=\frac{mg}{cos(α)}$
EQUILIBRIO ASSE X
Sull'asse X le forze orizzontali sono la forza elettrica e la componente orizzontale della tensione
$T_x-F=0$
Sostituiamo i valori delle due forze
$Tsin(α)-\frac{Kq^2}{4L^2sin^2(α)}=0$
Sostituiamo la tensione con l'equazione ricavata dall'equilibrio sull'asse Y
$\frac{mg}{cos(α)}\cdot sin(α)-\frac{Kq^2}{4L^2sin^2(α)}=0$
Sostituiamo il rapporto tra il seno e il coseno dell'angolo con la tangente dell'angolo $α$
$mg\cdot tg(α)-\frac{Kq^2}{4L^2sin^2(α)}=0$
Da questa equazione ricaviamo la carica delle due sferette
$mg\cdot tg(α)=\frac{Kq^2}{4L^2sin^2(α)}$
Moltiplichiamo entrambi i lati dell'equazione per $4L^2sin^2(α)/K$
$\frac{mg\cdot tg(α)\cdot 4L^2sin^2(α)}{K}=q^2$
Ora basta applicare la radice quadrata ad entrambi i lati dell'equazione per ricavare la carica delle due sfere
$q=±\sqrt{\frac{mg\cdot tg(α)\cdot 4L^2sin^2(α)}{K}}$
Ci sono due risultati possibili, uno in cui le due sferette sono entrambe positive e uno in cui sono entrambe negative
