Siccome i protoni hanno tutti la stessa carica e si trovano ognuno alla stessa distanza l'uno dall'altro, basta calcolare la forza totale agente su uno di loro per trovare la forza totale agente sugli altri.
La forza totale quindi sarà la somma della forza di repulsione tra il protone 1 e gli altri 3 protoni ai vertici del quadrato
$F=F_{1,2}+F_{1,3}+F_{1.4}$
Sostituendo con la formula della forza di Coulomb otteniamo:
$F=\frac{Kq_1q_2}{r_{1,2}^2}+\frac{Kq_1q_3}{r_{1,3}^2}+\frac{Kq_1q_4}{r_{1,4}^2}$
Le cariche sono tutte uguali, quindi scriviamo il prodotto delle due cariche come la carica del protone al quadrato, $q^2$. Inoltre dobbiamo sostituire ogni $r$ con la distanza tra ogni protone.
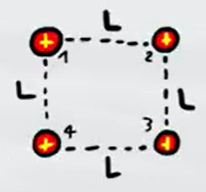
Come si vede dal disegno le distanze tra la carica 1 e le cariche 2 e 4 sono entrambe di $1m$ mentre la distanza tra la carica 1 e la carica 3 è la diagonale del quadrato di lato 1, quindi $r_{1,3}=\sqrt{2}m$
La forza totale diventa:
$F=\frac{Kq^2}{1^2}+\frac{Kq^2}{1^2}+\frac{Kq^2}{(\sqrt{2})^2}$
$F=\frac{5Kq^2}{2}$
La forza totale agente sul protone 1 può essere riscritta usata il secondo principio della dinamica
$F=ma$
Quindi l'equazione diventa
$ma=\frac{5Kq^2}{2}$
Da questa equazione possiamo ricavare l'accelerazione dei protoni
$a=\frac{5Kq^2}{2m}$
Dalle leggi orarie del moto rettilineo uniformemente accelerato possiamo ricavare la velocità sapendo che i protoni partono da fermi (velocità inziale uguale a 0)
$v=v_i+at$
$v=at$
Sostituendo l'accelerazione con quella ricavata otteniamo:
$v=\frac{5Kq^2}{2m}\cdot 1s=\frac{5Kq^2}{2m}$
Sostituendo i valori (sapendo che la massa del protone è $m=1,67\cdot 10^{-27}kg$) ricaviamo il valore della velocità:
$v=0,039$ $m/s$
