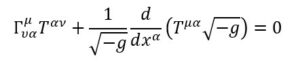Il tensore energia-impulso che descrive la distribuzione della massa e dell’energia all’interno del fluido (all’esterno il tensore vale 0) e viene definito in relatività ristretta in questo modo:
![]()
In cui p è la pressione e ρ la densità di energia
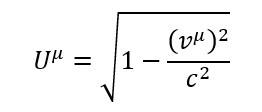
Come abbiamo mostrato in trasformare la relatività ristretta in relatività generale il tensore, in presenza di gravità diventa il seguente:
![]()
Inoltre in relatività ristretta vale la legge di continuità
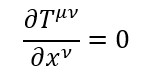
Che in relatività generale diventa una derivata covariante (ciò non implica una conservazione)
![]()
Quindi, applicando la definizione di derivata covariante, otteniamo
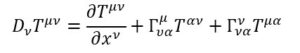
Siccome in relatività ristretta il tensore si conserva il primo termine è uguale a 0
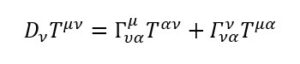
Dall’equazione ricavata in tensore metrico e connessione affine possiamo sostituire la seconda delta dell’equazione in questo modo:
![]()
Siccome il tensore metrico è una matrice possiamo usare la seguente regola per le matrici
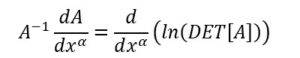
Quindi possiamo riscrivere la connessione affine così considerando il determinante come -g (perché il determinante del tensore metrico risulta negativo):
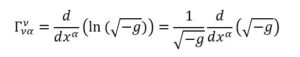
Mettendo questa connessione affine nell’equazione ottenuta dalla derivata covariante del tensore energia-impulso ottenendo: