Per ricavare la posizione della prima panda chiara e della terza banda scura dobbiamo calcolare le distanze tra le due bande e la banda centrale
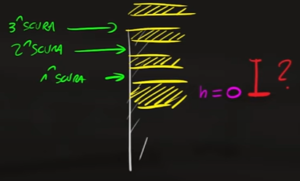
Dove $n=0$ rappresenta appunto la banda centrale.
Per ricavare la posizione delle due bande dobbiamo usare la seconda equazione delle fenditure
$y=Ltan(θ)$
Di questa equazione però non abbiamo l'angolo di inclinazione $θ$ delle due bande rispetto alla centrale che possiamo ricavare tramite la prima equazione delle fenditure
RICAVARE L'ANGOLO
La prima equazione delle fenditure è:
$dsin(θ)=n\frac{λ}{2}$
Dove $λ=200\cdot 10^{-9}$ $m$ e $d=0,02m$. $n$ invece è uguale a 2 per la prima banda chiara ed è uguale a 5 per la terza banda scura (questo perché tra una banda scura e un'altra c'è una banda chiara, per cui tra la banda centrale e la terza banda scura ci sono 4 bande: 2 chiare e 2 scure, mentre tra la banda centrale e la prima banda chiara c'è una banda scura).
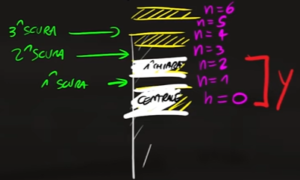
Da questa equazione ricaviamo il seno dell'angolo
$sin(θ)=\frac{nλ}{2d}$
Per ricavare $θ$ applichiamo la funzione inversa del seno
$θ=arcsin(\frac{nλ}{2d})$
Per la prima banda chiara $n=2$, quindi l'angolo di inclinazione è:
$θ_1=arcsin(\frac{2λ}{2d})=10^{-5}$ $rad$
Per la terza banda scura il numero vale $n=5$, quindi:
$θ_2=arcsin(\frac{5λ}{2d})=2,5\cdot 10^{-5}$ $rad$
SOLUZIONE
Ora che abbiamo i due angoli basta inserirli all'interno della seconda equazione per ricavare le due posizioni
$y_1=Ltan(θ_1)=2\cdot 10^{-5}$ $m$
$y_2=Ltan(θ_2)=5\cdot 10^{-5}$ $m$
Dove $L=2m$
