PAGINA DI TEORIA: Energia potenziale gravitazionale
La forza gravitazionale è una forza conservativa, quindi un corpo immerso in un campo gravitazionale scambia energia con il campo stesso. Questa energia scambiata è l'energia potenziale gravitazionale $U_g$
$U_g=-G\frac{m_1\cdot m_2}{r}$
Dove $m_1$ e $m_2$ sono le masse dei due corpi che scambiano energia gravitazionale, $r$ è la distanza tra i due corpi e $G$ è la costante di gravitazione universale
$G=6,67\cdot 10^{-11}N\cdot m^2/kg^2$
.
Il segno meno indica che per poter fuggire all'attrazione gravitazionale bisogna fornire energia al corpo.
Sommando la variazione di energia cinetica e di energia potenziale gravitazionale di un corpo possiamo trovare il lavoro totale:
$L=ΔE+ΔU$
Dove l'energia cinetica è data dal movimento del corpo ed è sempre:
$E=\frac{1}{2}mv^2$
Nel caso in cui non ci sia dispersione di energia cinetica o potenziale, il lavoro si conserva ($L=0$).
La velocità di fuga è la velocità minima necessaria per poter sfuggire all'attrazione gravitazionale di un corpo celeste, ciò avviene quando il lavoro totale è uguale a 0 e l'energia cinetica del corpo riesce a bilanciare l'energia potenziale gravitazionale.
$\frac{1}{2}m_1v^2-G\frac{m_1\cdot M}{r}=0$
Risolvendo l'equazione otteniamo:
$v=\sqrt{\frac{2GM}{r}}$
Dove $M$ è la massa del corpo celeste e $r$ il suo raggio
- Esercizio 1
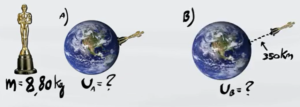
Calcola l'energia gravitazionale di un corpo di massa $m=8,8kg$ sulla Terra nelle seguenti posizioni:
a) Sulla superfice della Terra
b) Ad un altitudine di 350 km
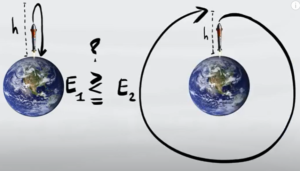
- Esercizio 2
L'energia necessaria per poter lanciare verticalmente un razzo fino ad un'altezza $h$ è maggiore minore o uguale all'energia necessaria per porre il razzo in un orbita alla stessa altezza?
- Esercizio 3
Calcola la velocità di fuga per sfuggire alla gravità di Mercurio e di Venere e stabilisci quale delle due è più grande

- Esercizio 4
Qual è l'energia cinetica minima che deve acquisire un razzo di massa $m=39.000kg$ per sfuggire alla gravità lunare? E per la gravità terrestre?

- Esercizio 5
La cometa di Halley compie una rivoluzione completa attorno al sole in un'orbita ellittica ogni 76 anni. Quando si trova in perielio la distanza dal centro del sole è $r_P=8,823\cdot 10^{10}m$ e quando si trova in afelio dista $r_A=6,152\cdot 10^{12}m$. La velocità in perielio è $v_P=54,6km/s$. La velocità in afelio è maggiore, minore o uguale alla velocità in perielio?

- Esercizio 6
Un satellite di massa $m$ orbita attorno ad un pianeta di massa $M$ in un orbita circolare di raggio $r$ e con periodo di rivoluzione $T$. Trova le equazioni che descrivono la massa $M$ del pianeta e l'energia totale del satellite