Dai dati abbiamo che la somma di energia cinetica e potenziale della tuffatrice è
$ΔE+ΔU=-5120J$
ENERGIA CINETICA
Nel tuffo possiamo porre che la tuffatrice parta da ferma, quindi ha energia cinetica inziale nulla
$E_i=0$
Inoltre la tuffatrice è ferma anche alla fine del tuffo, quindi l'energia cinetica finale è anch'essa 0
$E_f=0$
Per cui l'energia cinetica totale è 0. Quindi l'energia totale è uguale all'energia potenziale
$ΔU=-5120J$
ENERGIA POTENZIALE
Se poniamo come sistema di riferimento il livello dell'acqua abbiamo che la distanza percorsa sott'acqua è negativa
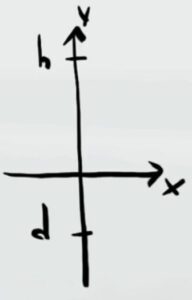
Quindi l'energia potenziale inziale è data dall'altezza del trampolino rispetto al livello dell'acqua (cioè $h$ come riportato dai dati)
$U_i=mgh$
L'energia potenziale finale invece è negativa, perché la distanza tra l'altezza $d$ e il livello dell'acqua è negativo
$U_f=mg(-d)=-mgd$
L'energia potenziale totale è la differenza di queste due ed è uguale a $E_{tot}=-5120J$
$U_f-U_i=-5120J$
$-mgd-mgh=5120J$
Da questa equazione ricaviamo l'incognita $d$
$mgd=5120-mgh$
$d=\frac{5120-mgh}{mg}=2,49m$
