PAGINA DI TEORIA: ENERGIA CINETICA
L'energia cinetica è l'energia posseduta da un corpo a causa del suo movimento. La formula dell'energia cinetica è
$E=\frac{1}{2}mv^2$
L'energia cinetica totale di un corpo è la differenza tra energia cinetica nell'istante finale ed energia cinetica nell'istante inziale
$ΔE=\frac{1}{2}mv_{f}^2-\frac{1}{2}mv_{i}^2$
In assenza di energie potenziali (cioè energie derivate dall'interazione con campi di forze come la forza gravitazionale o elettrica), l'energia cinetica è uguale al lavoro compiuto dal corpo
$L=ΔE$
Dove il lavoro è
$L=FΔx$
Il teorema di conservazione dell'energia cinetica afferma che, in un sistema isolato dove non sono presenti forze esterne come la forza di attrito, l'energia cinetica scambiata tra due o più corpi è uguale nel tempo
$E_{inziale}=E_{finale}$
Dove l'energia inziale e l'energia finale sono la somma delle energie cinetiche di tutti i corpi. Per due corpi che scambiano energia cinetica (cioè urtano tra loro) somma è
$E_{i_1}+E_{i_2}=E_{f_1}+E_{f_2}$
Sostituendo le energie con la formula dell'energia cinetica otteniamo
$\frac{1}{2}m_1v_{1i}^2+\frac{1}{2}m_2v_{2i}^2=\frac{1}{2}m_1v_{1f}^2+\frac{1}{2}m_2v_{2f}^2$
- Esercizio 1
Determinare l'energia cinetica acquisita da un razzo di massa $m=5\cdot 10^5 kg$ quando raggiunge la velocità minima per sfuggire all'orbita terrestre $v=11,2 km/s$
- Esercizio 2
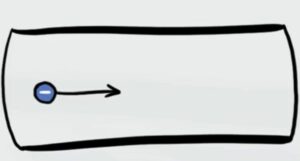
Un elettrone di massa $m=9,11\cdot 10^{-31} kg$ in un acceleratore di particelle si muove con accelerazione $a=10^{15} m/s^2$. Calcola quanta energia cinetica guadagna l'elettrone quando entra in una zona lunga 10 centimetri con velocità di entrata $v_i=2\cdot 10^7 m/s$.
- Esercizio 3
Un corpo di massa $m=20 kg$ si muove inizialmente a velocità costante $v=10 m/s$. Per poterlo fermare viene fatto decelerare con $a=-2 m/s^2$.
a) Calcola la forza necessaria per fermarlo
b) Calcola la distanza percorsa durante il rallentamento
c) Calcola il lavoro totale del corpo
- Esercizio 4
Su un corpo inizialmente fermo di massa $m=5 kg$ agiscono 3 forze di intensità $F_1=1 N$, $F_2=2N$ e $F_3=3N$ e sono disposte come mostrato in figura.
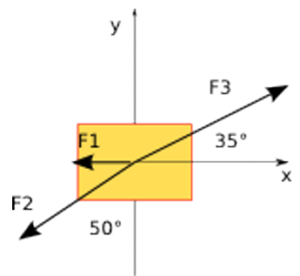
Calcola l'energia cineta finale del corpo dopo 4 secondi.
- Esercizio 5
Una macchina di massa $m_A=732kg$ inizialmente ferma, viene tamponata da un furgone di massa $m_F=1720kg$ che va ad una velocità $v_F=15,5m/s$. L'urto è completamente elastico.
Calcola la velocità del furgone e della macchina dopo l'urto.
NOTA: il problema richiede le equazioni della quantità di moto dei due corpi

- Esercizio 6
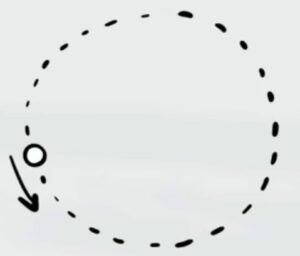
Un corpo di massa $m=1 kg$ si muove di moto circolare uniforme attorno ad un punto materiale con frequenza $f= 2 Hz$. La distanza tra il corpo e il punto materiale è $d=1 m$.
a) Quanto vale l'energia cinetica del corpo?
b) Se il corpo inizia a decelerare con accelerazione $a=-1 m/s^2$. Quanto vale lo spostamento angolare totale prima di fermarsi?